Доказательство.
Пусть 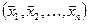 есть ортогональная система ненулевых векторов евклидова пространства. Предположим, что выполняется равенство
есть ортогональная система ненулевых векторов евклидова пространства. Предположим, что выполняется равенство 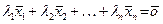 . Умножим скалярно обе части этого равенства последовательно на векторы
. Умножим скалярно обе части этого равенства последовательно на векторы 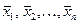 .
.
Тогда, например, для произведения на первый вектор системы получим:
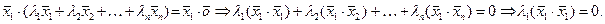
Так как векторы системы ненулевые то 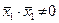 и, следовательно,
и, следовательно, 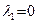 . Аналогично показывается, что и все остальные числовые коэффициенты линейной комбинации равны нулю, что и доказывает линейную независимость векторов ортогональной системы.
. Аналогично показывается, что и все остальные числовые коэффициенты линейной комбинации равны нулю, что и доказывает линейную независимость векторов ортогональной системы.
Система векторов называется нормированной, если она состоит только из нормированных векторов. Любую систему ненулевых векторов можно нормировать, если каждый из векторов умножить на число, обратное модулю этого вектора.
Определение.Система векторов 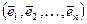 евклидова пространства называется ортонормированной, если все ее векторы нормированы и попарно ортогональны.
евклидова пространства называется ортонормированной, если все ее векторы нормированы и попарно ортогональны.
В евклидовом пространстве арифметических векторов 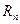 система канонических векторов
система канонических векторов 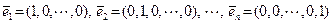 является ортонормированной при любой размерности пространства
является ортонормированной при любой размерности пространства  , что проверяется непосредственно по определениям.
, что проверяется непосредственно по определениям.