Теорема Грама-Шмидта (о существовании ортонормированного базиса).
Во всяком 
 -мерном евклидовом пространстве
-мерном евклидовом пространстве 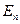 существует ортонормированный базис
существует ортонормированный базис 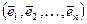 .
.
Доказательство.Согласно аксиоме размерности в пространстве 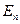 имеется линейно независимая система из
имеется линейно независимая система из  векторов
векторов 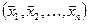 . Покажем, что можно построить систему из
. Покажем, что можно построить систему из  векторов
векторов 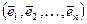 линейно выражающихся через векторы системы
линейно выражающихся через векторы системы 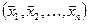 , и образующих ортонормированный базис.
, и образующих ортонормированный базис.
Доказательство проведем по методу математической индукции.
1. При 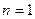 утверждение теоремы очевидно. Если
утверждение теоремы очевидно. Если 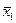 есть ненулевой вектор, то один нормированный вектор
есть ненулевой вектор, то один нормированный вектор 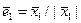 образует ортонормированный базис.
образует ортонормированный базис.
2. Предположим, что в каждом 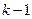 - мерном евклидовом пространстве существует ортонормированный базис, и докажем то же утверждение для произвольного
- мерном евклидовом пространстве существует ортонормированный базис, и докажем то же утверждение для произвольного 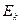 .
.
Пусть 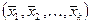 есть произвольный базис в пространстве
есть произвольный базис в пространстве 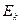 . Линейная оболочка векторов системы
. Линейная оболочка векторов системы 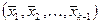 представляет собой евклидово пространство размерности
представляет собой евклидово пространство размерности 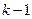 и, по предположению индукции, там существует ортонормированная система из
и, по предположению индукции, там существует ортонормированная система из 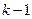 векторов
векторов 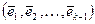 . Построим новый
. Построим новый 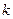 -тый вектор
-тый вектор 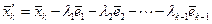 .
.
Коэффициенты 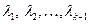 выберем такими, чтобы новый вектор был ортогонален всем векторам системы
выберем такими, чтобы новый вектор был ортогонален всем векторам системы 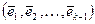 . Так как система
. Так как система 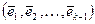 является ортонормированной, получим
является ортонормированной, получим 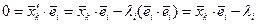 , откуда
, откуда 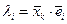 для всех
для всех 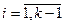 .
.
Нормируем вектор 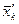 , т.е. построим единичный вектор
, т.е. построим единичный вектор 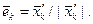 По построению вектор
По построению вектор 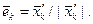 ортогонален векторам системы
ортогонален векторам системы 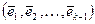 и имеет единичную длину. Таким образом, найдена ортонормированная система векторов
и имеет единичную длину. Таким образом, найдена ортонормированная система векторов 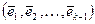 , которая линейно независима и является базисом евклидова пространства
, которая линейно независима и является базисом евклидова пространства 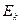 . На этом завершается доказательство теоремы Грамма-Шмидта по методу математической индукции.
. На этом завершается доказательство теоремы Грамма-Шмидта по методу математической индукции.
Конструктивный метод, с помощью которого был построен ортонормированный базис при доказательстве теоремы, называют методом ортогонализации Грама-Шмидта.
При практической реализации метода Грама-Шмидта, отправляясь от системы векторов 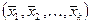 , последовательно находят ортонормированные векторы
, последовательно находят ортонормированные векторы  в соответствии со следующим алгоритмом:
в соответствии со следующим алгоритмом:
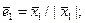
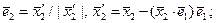
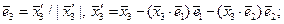
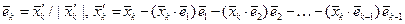
Отметим, что в каждом евклидовом пространстве существует бесконечно много ортонормированных базисов. Так, начиная процесс ортогонализации с любого ненулевого вектора, можно построить некоторый ортонормированный базис.