Теорема (условие равенства векторного произведения нулевому вектору).
Векторное произведение двух геометрических векторов  и
и 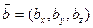 равно нулевому вектору, тогда и только тогда, когда векторы
равно нулевому вектору, тогда и только тогда, когда векторы  и
и 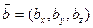 являются коллинеарными.
являются коллинеарными.
Доказательство.Если хотя бы один из векторов  ,
, 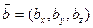 равен нулевому вектору
равен нулевому вектору 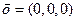 , то векторное произведение также равно нулевому вектору.
, то векторное произведение также равно нулевому вектору.
В том случае, когда оба вектора  ,
,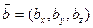 отличны от нулевого и являются коллинеарными, их компоненты должны быть пропорциональными, так что
отличны от нулевого и являются коллинеарными, их компоненты должны быть пропорциональными, так что  . Из определения векторного произведения следует, что и в этом случае векторное произведение равно нулевому вектору. Таким образом, доказана достаточность условия теоремы.
. Из определения векторного произведения следует, что и в этом случае векторное произведение равно нулевому вектору. Таким образом, доказана достаточность условия теоремы.
Для доказательства необходимости условия теоремы, предположим, что векторное произведение равно нулевому вектору. Из условия равенства векторов следует, что 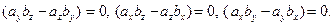 Эти равенства означают, что компоненты векторов
Эти равенства означают, что компоненты векторов  и
и 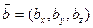 пропорциональна, а сами векторы являются коллинеарными, что и требовалось доказать.
пропорциональна, а сами векторы являются коллинеарными, что и требовалось доказать.
Из доказанной теоремы, по закону контрпозиции, вытекает следствие.
Следствие.Векторное произведение  не равно нулевому вектору, тогда и только тогда, когда векторы
не равно нулевому вектору, тогда и только тогда, когда векторы  ,
,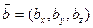 не являются коллинеарными.
не являются коллинеарными.