Теорема (о модуле векторного произведения ).
Модуль векторного произведения двух векторов  и
и 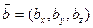 может вычисляться по формуле
может вычисляться по формуле 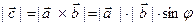 , где
, где  есть угол между векторами
есть угол между векторами 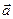 и
и 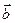 . Если векторы
. Если векторы 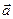 ,
, 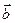 не являются коллинеарными, то модуль векторного произведения равен площади параллелограмма, построенного на векторах
не являются коллинеарными, то модуль векторного произведения равен площади параллелограмма, построенного на векторах 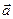 и
и 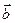 .
.
Доказательство.Если векторы  ,
, 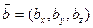 являются коллинеарными, то их векторное произведение равно нулевому вектору, а модуль нулевого вектора равен нулю. Так как угол между коллинеарными векторами равен 0 или
являются коллинеарными, то их векторное произведение равно нулевому вектору, а модуль нулевого вектора равен нулю. Так как угол между коллинеарными векторами равен 0 или 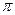 , то
, то 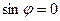 .
.
Таким образом, доказываемая формула справедлива для коллинеарных векторов.
Пусть векторы 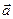 и
и 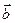 не являются коллинеарными.
не являются коллинеарными.
Обозначим направляющие косинусы вектора 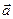 как
как 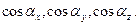 Так как, по определению, направляющие косинусы есть компоненты орта вектора
Так как, по определению, направляющие косинусы есть компоненты орта вектора 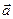 , то для них справедлива формула
, то для них справедлива формула 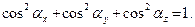 Компоненты вектора
Компоненты вектора 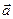 выражаются через модуль вектора
выражаются через модуль вектора 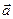 и направляющие косинусы по формулам
и направляющие косинусы по формулам 
Аналогично, обозначим направляющие косинусы вектора 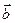 как
как 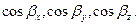 Для них также справедлива формула
Для них также справедлива формула 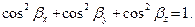 Кроме того, выполняются равенства для компонент вектора
Кроме того, выполняются равенства для компонент вектора 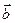 в виде
в виде 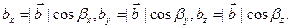
Косинус угла  между векторами
между векторами 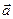 и
и 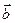 вычисляется как скалярное произведение между их ортами по формуле
вычисляется как скалярное произведение между их ортами по формуле 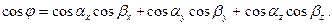
Найдем далее квадрат модуля векторного произведения:
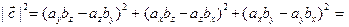
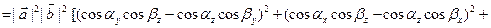
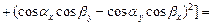
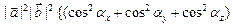

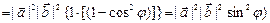 .
.
Отсюда следует  , что и завершает доказательство первой части теоремы.
, что и завершает доказательство первой части теоремы.
Если векторы 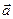 ,
, 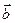 не являются коллинеарными, то на них можно построить параллелограмм. Площадь любого параллелограмм вычисляется как произведение длины основания параллелограмма на его высоту. В нашем случае длина основания равна
не являются коллинеарными, то на них можно построить параллелограмм. Площадь любого параллелограмм вычисляется как произведение длины основания параллелограмма на его высоту. В нашем случае длина основания равна  , а высота равна
, а высота равна 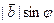 . Таким образом, теорема полностью доказана.
. Таким образом, теорема полностью доказана.
Определение.Векторно-скалярным или смешанным произведением трех упорядоченных векторов  ,
, 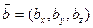 ,
, 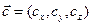 в реальном пространстве называют число, найденное по правилу
в реальном пространстве называют число, найденное по правилу  , где для первых двух векторов составляется векторное произведение, которое затем скалярно умножается на третий вектор.
, где для первых двух векторов составляется векторное произведение, которое затем скалярно умножается на третий вектор.
Учитывая определения векторного и скалярного произведений, значение смешанного произведения вычисляют по формуле
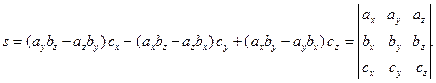
Если векторы  ,
, 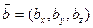 ,
, 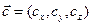 являются компланарными, то один из векторов, может быть представлен в виде линейной комбинации двух других. В этом случае одна из строк определителя смешанного произведения будет линейной комбинацией двух других строк. Как известно, значение такого определителя равно нулю.
являются компланарными, то один из векторов, может быть представлен в виде линейной комбинации двух других. В этом случае одна из строк определителя смешанного произведения будет линейной комбинацией двух других строк. Как известно, значение такого определителя равно нулю.