Теорема (об условиях равенства нулю произведения числа на вектор).
Произведение числа на вектор равно нулевому вектору тогда и только тогда, когда число равно нулю или вектор равен нулевому вектору.
Доказательство.Пусть число  равно нулю или вектор
равно нулю или вектор  является нулевым. Покажем, что
является нулевым. Покажем, что  . Пусть вначале
. Пусть вначале  . Справедливо
. Справедливо  . В силу единственности нулевого вектора отсюда следует
. В силу единственности нулевого вектора отсюда следует  . Если
. Если  , то рассмотрим равенства
, то рассмотрим равенства  . Снова, в силу единственности нулевого вектора, следует
. Снова, в силу единственности нулевого вектора, следует 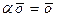 .
.
Обратно, пусть  . Покажем, что
. Покажем, что  или
или  . Доказательство проведем методом от обратного. Предположим, что равенство
. Доказательство проведем методом от обратного. Предположим, что равенство  истинно, а заключение
истинно, а заключение  или
или  ложное, т.е. справедливо
ложное, т.е. справедливо  и
и  . Тогда по предположению и уже доказанной первой части нашей теоремы получим
. Тогда по предположению и уже доказанной первой части нашей теоремы получим  .
.
С другой стороны, по нашему предположению и аксиомам  имеем
имеем  . Полученное противоречие доказывает вторую часть теоремы.
. Полученное противоречие доказывает вторую часть теоремы.
Из доказанных выше теорем выведем еще два следствия.
4.Для любого вектора  из
из 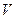 противоположный вектор
противоположный вектор  равен
равен  .
.
Действительно,  Отсюда, в силу единственности противоположного вектора, получаем доказательство следствия.
Отсюда, в силу единственности противоположного вектора, получаем доказательство следствия.
5. Для любого вектора  противоположный вектор к противоположному
противоположный вектор к противоположному  равен исходному вектору, т.е.
равен исходному вектору, т.е.  .
.
Действительно,  , что и утверждается в следствии.
, что и утверждается в следствии.