ОПРЕДЕЛИТЕЛИ МАТРИЦ И ИХ СВОЙСТВА
Определители вводятся только для квадратных матриц как некоторое правило, формирующее значение определителя по элементам матрицы. Если элементы матрицы числа, то определитель будет числом; если элементы матрицы функции, то и определитель будет функцией и так далее. Обозначается определитель любой квадратной матрицы  одним из следующих символов
одним из следующих символов 
 . Определяющее правило составления определителя введем индуктивно, то есть будем выражать значение определителя матрицы размера
. Определяющее правило составления определителя введем индуктивно, то есть будем выражать значение определителя матрицы размера 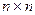 (определитель порядка
(определитель порядка  ) через определители меньших порядков.
) через определители меньших порядков.
Определитель  матрицы
матрицы  положим равным элементу
положим равным элементу 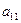 . Так, например,
. Так, например,  .
.
Определителем порядка  назовем число, которое будем находить по правилу разложения по первой строке матрицы
назовем число, которое будем находить по правилу разложения по первой строке матрицы 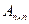 размера
размера 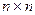 :
:
 .
.
В этой и во всех последующих формулах минором  элемента
элемента 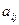 называется определитель порядка
называется определитель порядка  , полученный вычеркиванием из исходной матрицы строки с номером
, полученный вычеркиванием из исходной матрицы строки с номером 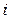 и столбца с номером
и столбца с номером 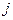 . Отсюда определитель второго порядка находится по правилу
. Отсюда определитель второго порядка находится по правилу
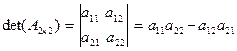 ,
,
т. е. составляется разность произведений элементов, стоящих на главной диагонали, и элементов, стоящих на побочной диагонали.
Так 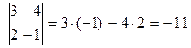 ,
, 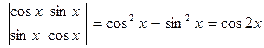 .
.
Определитель третьего порядка по общей формуле сначала выражается через определители второго порядка и далее определители первого порядка:
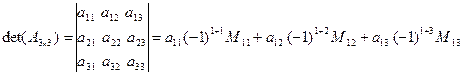 =
=
=  =
=
=  .
.
Если в последнем выражении определителя третьего порядка в одну группу собрать произведения со знаком плюс, а во вторую – произведения со знаком минус, то мы получим формулу раскрытия определителя по правилу Саррюса:
 =
=
(определитель третьего порядка равен сумме произведений его элементов, находящихся на главной диагонали и в вершинах равнобедренных треугольников, основания которых параллельны главной диагонали, минус сумму произведений элементов, находящихся на побочной диагонали и в вершинах равнобедренных треугольников, основания которых параллельны побочной диагонали).
Вычислим по правилу Саррюса следующий определитель третьего порядка
 =
=
=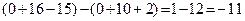 .
.
В теории определителей важную роль играет следующая основная теорема, которую мы приводим без доказательства. Определим, предварительно, алгебраическое дополнение 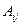 любого элемента
любого элемента 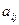 по формуле
по формуле
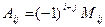 .
.
Как следует из определяющей формулы, алгебраическое дополнение может отличаться от минора только знаком.