рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Линейная зависимость функций. Определитель Вронского
Реферат Курсовая Конспект
Линейная зависимость функций. Определитель Вронского
Линейная зависимость функций. Определитель Вронского - раздел Математика, Математический анализ Перейдем К Более Глубокому Изучению Свойств Векторного Пространства Решений У...
Перейдем к более глубокому изучению свойств векторного пространства решений уравнения  (2). Мы установим ниже, что оно имеет размерность
(2). Мы установим ниже, что оно имеет размерность  .
.
Определение. Пусть 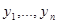 - функции, имеющие все производные до
- функции, имеющие все производные до  порядка включительно. Определителем Вронского
порядка включительно. Определителем Вронского 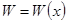 функций
функций 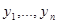 называется величина
называется величина 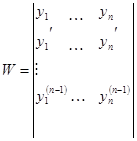 (3).
(3).
Определение. Пусть 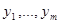 определены ны интервале
определены ны интервале 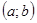 . Мы назовем их линейно зависимыми, если существуют постоянные
. Мы назовем их линейно зависимыми, если существуют постоянные 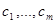 , не все равные 0, такие, что для всех
, не все равные 0, такие, что для всех 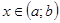
 (4).
(4).
Функции, которые не являются линейно зависимыми, называются линейно независимыми. Линейная независимость означает, что из равенства (4) следует, что 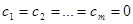 .
.
Теорема 5. Если 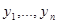 - линейно зависимы и имеют производные до
- линейно зависимы и имеют производные до  порядка включительно, то
порядка включительно, то 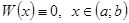 .
.
Доказательство. По условию, существуют не все равные 0 числа 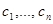 такие, что на
такие, что на 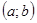 выполняется тождество
выполняется тождество  (5). Взяв производную от обеих частей, получим:
(5). Взяв производную от обеих частей, получим: 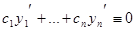 (6). Аналогично,
(6). Аналогично, 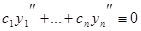 , (7)
, (7)  (8).
(8).
Рассмотрим произвольное 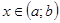 . Равенства (5) – (8) можно рассматривать как систему линейных однородных уравнений относительно неизвестных
. Равенства (5) – (8) можно рассматривать как систему линейных однородных уравнений относительно неизвестных 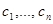 . Поскольку эта система имеет нетривиальное решение
. Поскольку эта система имеет нетривиальное решение 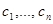 (это означает, что не все
(это означает, что не все 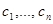 равны 0), ее определитель
равны 0), ее определитель 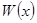 должен быть равен 0, т.е.
должен быть равен 0, т.е. 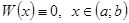 .
.
Обратная теорема в общем случае неверна. Рассмотрим, например, функции 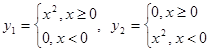 , для которых
, для которых  и их определитель Вронского
и их определитель Вронского 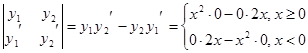 тождественно равен 0.
тождественно равен 0.
Однако если  , то при любом
, то при любом 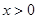 получаем
получаем 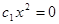 , откуда
, откуда 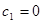 , а при любом
, а при любом 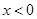 получаем
получаем 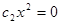 , откуда
, откуда 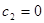 . Поэтому функции
. Поэтому функции  и
и  линейно независимы.
линейно независимы.
Тем не менее, верна следующая важная теорема.
Теорема 6. Если 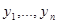 являются решением уравнения (2) и в некоторой точке
являются решением уравнения (2) и в некоторой точке 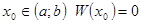 , то
, то 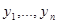 линейно зависимы на
линейно зависимы на 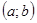 (и, следовательно,
(и, следовательно, 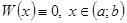 ).
).
Доказательство. Рассмотрим систему линейных уравнений относительно неизвестных 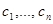 :
: 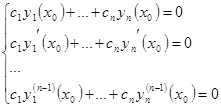 (9). Ее определитель равен
(9). Ее определитель равен  . По условию,
. По условию,  . Значит, система (9) имеет нетривиальное решение
. Значит, система (9) имеет нетривиальное решение 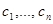 . Рассмотрим функцию
. Рассмотрим функцию 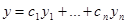 . По теореме 1,
. По теореме 1, 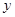 является решением уравнения (2). Равенства (9) можно рассматривать как условия задачи Коши,
является решением уравнения (2). Равенства (9) можно рассматривать как условия задачи Коши, 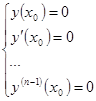 , которая, по теореме 1, имеет единственное решение. Вместе с тем, функция
, которая, по теореме 1, имеет единственное решение. Вместе с тем, функция 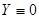 также удовлетворяет уравнению (2) и условиям (10). Ввиду единственности,
также удовлетворяет уравнению (2) и условиям (10). Ввиду единственности, 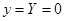 . Таким образом, существуют не все равные 0 постоянные
. Таким образом, существуют не все равные 0 постоянные 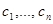 такие, что
такие, что  . Поэтому
. Поэтому 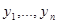 - линейно зависимы на
- линейно зависимы на 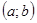 . Следовательно, по теореме 5,
. Следовательно, по теореме 5, 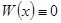 на
на 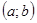 .
.
– Конец работы –
Эта тема принадлежит разделу:
Математический анализ
На сайте allrefs.net читайте: "Математический анализ"
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Линейная зависимость функций. Определитель Вронского
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов