рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Метод неопределенных коэффициентов для нахождения частного решения линейного неоднородного дифференциального уравнения с постоянными коэффициентами
Реферат Курсовая Конспект
Метод неопределенных коэффициентов для нахождения частного решения линейного неоднородного дифференциального уравнения с постоянными коэффициентами
Метод неопределенных коэффициентов для нахождения частного решения линейного неоднородного дифференциального уравнения с постоянными коэффициентами - раздел Математика, Математический анализ Согласно Общей Теории Линейных Дифференциальных Уравнений, Для Решения Уравне...
Согласно общей теории линейных дифференциальных уравнений, для решения уравнения  (1) достаточно знать фундаментальную систему решений
(1) достаточно знать фундаментальную систему решений 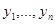 однородного уравнения
однородного уравнения  (2) и найти хотя бы одно решение
(2) и найти хотя бы одно решение  неоднородного уравнения. Тогда любое решение
неоднородного уравнения. Тогда любое решение 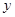 неоднородного уравнения имеет вид:
неоднородного уравнения имеет вид:  , где
, где 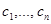 - произвольные постоянные.
- произвольные постоянные.
В случае уравнения с постоянными коэффициентами мы указали способы нахождения его фундаментальной системы решений. Используя метод вариации постоянных, можно теперь найти решение и неоднородного уравнения. Однако есть важные частные случаи, когда решение неоднородного уравнения можно отыскать значительно проще.
Пусть  (3), где
(3), где 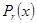 - многочлены,
- многочлены,  - действительные числа. Согласно принципу суперпозиции, достаточно уметь решать уравнение вида
- действительные числа. Согласно принципу суперпозиции, достаточно уметь решать уравнение вида 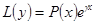 (4). Тогда, решив каждое из уравнений
(4). Тогда, решив каждое из уравнений 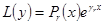 и просуммировав полученные решения, мы получим решение исходного уравнения (3).
и просуммировав полученные решения, мы получим решение исходного уравнения (3).
Решения уравнения (4) имеют различный вид в зависимости от того, является или нет число  корнем характеристического уравнения для однородного уравнения (2).
корнем характеристического уравнения для однородного уравнения (2).
В первом случае  не является корнем характеристического уравнения. Тогда решение уравнения (4) можно искать в виде
не является корнем характеристического уравнения. Тогда решение уравнения (4) можно искать в виде  , где
, где  - многочлен той же степени, что и многочлен
- многочлен той же степени, что и многочлен 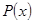 .
.
Во втором случае, если  является корнем характеристического уравнения (2) кратности
является корнем характеристического уравнения (2) кратности  , решение уравнения (4) следует искать в виде
, решение уравнения (4) следует искать в виде 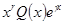 , где
, где  - многочлен той же степени, что и
- многочлен той же степени, что и 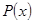 .
.
Эти два случая можно объединить в один, если считать, что  , не являющееся корнем характеристического уравнения, имеет нулевую кратность. Тогда решение уравнения (4) следует искать в виде
, не являющееся корнем характеристического уравнения, имеет нулевую кратность. Тогда решение уравнения (4) следует искать в виде 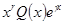 ,
, 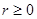 , где
, где  - кратность
- кратность  в характеристическом уравнении.
в характеристическом уравнении.
Если в правую часть  уравнения (1) входят слагаемые вида
уравнения (1) входят слагаемые вида  (5), где
(5), где  - многочлены, то можно искать решение уравнений
- многочлены, то можно искать решение уравнений 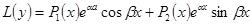 (6) в виде
(6) в виде  , где
, где  - кратность корня
- кратность корня 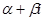 в характеристическом многочлене однородного уравнения (
в характеристическом многочлене однородного уравнения ( , если
, если 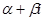 - не корень характеристического уравнения), а степень каждого из многочленов
- не корень характеристического уравнения), а степень каждого из многочленов  равна наивысшей из степеней многочленов
равна наивысшей из степеней многочленов  .
.
Когда слагаемых вида (5) несколько, то мы решаем соответствующие им уравнения (6) и применяем затем принцип суперпозиции.
Рассмотрим важный пример.
Пример. Уравнение упругих колебаний без сопротивления при наличии возмущающей периодической силы:  ,
, 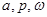 - постоянные.
- постоянные.
Корни характеристичского уравнения  равны
равны  . Поэтому фундаментальная система решений однородного уравнения
. Поэтому фундаментальная система решений однородного уравнения 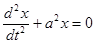 состоит из функций
состоит из функций 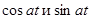 .
.
Если 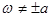 , то решение исходного уравнения ищем в виде
, то решение исходного уравнения ищем в виде  . Подставляем его в уравнение:
. Подставляем его в уравнение:  ,
,  , откуда
, откуда 
 , или
, или  , откуда
, откуда 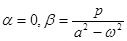 . Тем самым, общее решение уравнения имеет вид
. Тем самым, общее решение уравнения имеет вид  . Здесь
. Здесь  - амплитуда свободных колебаний,
- амплитуда свободных колебаний,  - частота свободных колебаний,
- частота свободных колебаний,  - амплитуда вынужденных колебаний с частотой
- амплитуда вынужденных колебаний с частотой  . Чем ближе величина
. Чем ближе величина 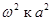 , тем больше амплитуда вынужденных колебаний.
, тем больше амплитуда вынужденных колебаний.
Если же  , то решение, согласно указанным выше правилам, следует искать в виде
, то решение, согласно указанным выше правилам, следует искать в виде 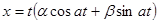 . Тогда
. Тогда 
 . Подставим в уравнение:
. Подставим в уравнение: 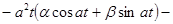
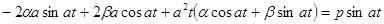 , или
, или  . Итак, общее решение уравнения имеет вид:
. Итак, общее решение уравнения имеет вид:  . При
. При 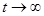 амплитуда колебаний возрастает неограниченно. Это – явление резонанса.
амплитуда колебаний возрастает неограниченно. Это – явление резонанса.
– Конец работы –
Эта тема принадлежит разделу:
Математический анализ
На сайте allrefs.net читайте: "Математический анализ"
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Метод неопределенных коэффициентов для нахождения частного решения линейного неоднородного дифференциального уравнения с постоянными коэффициентами
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов