рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Доказательство.
Реферат Курсовая Конспект
Доказательство.
Доказательство. - раздел Математика, Математический анализ . Пусть ...
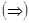 . Пусть
. Пусть  . Тогда
. Тогда 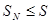 при всех
при всех  .
.
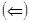 . Пусть
. Пусть  . Поскольку
. Поскольку 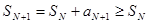 , последовательность
, последовательность  возрастает и, по условию, ограничена. Следовательно, по теореме Вейерштрасса (см. 1-ый семестр), она имеет предел, то есть ряд сходится.
возрастает и, по условию, ограничена. Следовательно, по теореме Вейерштрасса (см. 1-ый семестр), она имеет предел, то есть ряд сходится.
Простые следствия из этого критерия – очень полезные теоремы сравнения.
Теорема 1. Пусть для всех 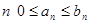 и пусть ряд
и пусть ряд 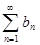 - сходится. Тогда сходится ряд
- сходится. Тогда сходится ряд 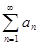 .
.
Доказательство. Очевидны неравенства  . По условию
. По условию 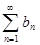 - сходится. Значит, по приведенному выше критерию,
- сходится. Значит, по приведенному выше критерию, 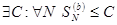 . Но тогда и
. Но тогда и  и, значит, ряд
и, значит, ряд 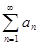 - сходится.
- сходится.
Примечание 1. Эта теорема может быть сформулирована и так: Пусть для всех 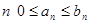 и ряд
и ряд 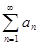 - расходится, тогда расходится и ряд
- расходится, тогда расходится и ряд 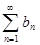 . Действительно, если бы этот ряд сходился, то первой теореме должен был бы сходиться и ряд
. Действительно, если бы этот ряд сходился, то первой теореме должен был бы сходиться и ряд 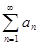 .
.
Примечание 2. Теорема 1 справедлива и в случае, когда неравенство 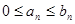 выполняется начиная с некоторого номера
выполняется начиная с некоторого номера  .
.
Теорема 2. Пусть  для всех
для всех  и
и 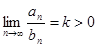 . Тогда либо оба ряда
. Тогда либо оба ряда 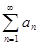 и
и 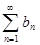 сходятся, либо они оба расходятся. (Т.е. не может быть так, что один из них сходится, а другой расходится).
сходятся, либо они оба расходятся. (Т.е. не может быть так, что один из них сходится, а другой расходится).
Доказательство.  . Выберем
. Выберем 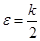 . Тогда
. Тогда  (т.к.
(т.к. 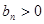 )
)  при
при  .
.
Если ряд 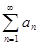 – сходится, то сходится и ряд
– сходится, то сходится и ряд  (по примечанию 2 к теореме 1). Тогда, взяв
(по примечанию 2 к теореме 1). Тогда, взяв  , получим, что и ряд
, получим, что и ряд 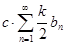 , т.е. ряд
, т.е. ряд 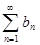 – сходится.
– сходится.
Если ряд 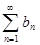 – сходится, то сходится и ряд
– сходится, то сходится и ряд  и, следовательно, сходится ряд
и, следовательно, сходится ряд 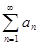 .
.
Теорема доказана.
Пример применения теоремы 2. Ряд 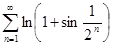 сходится, т.к.
сходится, т.к. 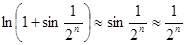 при
при 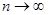 и ряд
и ряд  – сходится.
– сходится.
Теорема. (Признак сходимости Коши). Пусть 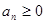 и при достаточно больших
и при достаточно больших 
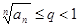 . Тогда ряд
. Тогда ряд 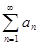 сходится. Если же при
сходится. Если же при 
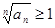 , то он расходится.
, то он расходится.
Доказательство. Неравенство 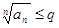 при
при  равносильно неравенству
равносильно неравенству  . Так как
. Так как 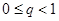 , ряд
, ряд  – сходится. По теореме 1 из предыдущего параграфа ряд
– сходится. По теореме 1 из предыдущего параграфа ряд 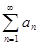 также сходится.
также сходится.
Если же  , то и
, то и 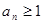 и равенство
и равенство 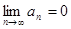 невозможно. Т.о. необходимый признак сходимости не выполняется и ряд расходится.
невозможно. Т.о. необходимый признак сходимости не выполняется и ряд расходится.
В предельной форме эта теорема выглядит так:
Теорема. Пусть существует  . Тогда если
. Тогда если 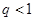 – ряд сходится,
– ряд сходится, 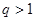 – ряд расходится,
– ряд расходится, 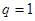 – признак неприменим.
– признак неприменим.
Доказательство. Пусть 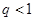 . Выберем
. Выберем  так, чтобы
так, чтобы  (т.е.
(т.е.  ). Тогда при
). Тогда при 
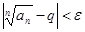 , т.е.
, т.е. 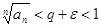 . Применяя предыдущую теорему получаем, что ряд сходится.
. Применяя предыдущую теорему получаем, что ряд сходится.
Если же 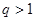 , то выберем
, то выберем  так, что
так, что 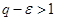 (т.е.
(т.е. 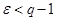 ). Тогда
). Тогда  . Вновь по предыдущей теореме ряд расходится.
. Вновь по предыдущей теореме ряд расходится.
Теорема. (Признак сходимости Даламбера). Пусть при всех 
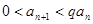 , где
, где 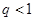 . Тогда ряд сходится. Если же при
. Тогда ряд сходится. Если же при 
 , то ряд расходится.
, то ряд расходится.
Доказательство. Из условий теоремы следует 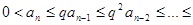
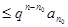 . Иными словами,
. Иными словами, 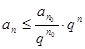 и по первой теореме сравнения ряд сходится.
и по первой теореме сравнения ряд сходится.
Если  , то
, то 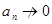 при
при 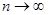 и ряд расходится.
и ряд расходится.
В предельной форме этот признак выглядит так:
Теорема. Если существует  , то при
, то при 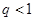 ряд сходится, при
ряд сходится, при 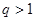 - расходится, а при
- расходится, а при 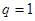 признак неприменим.
признак неприменим.
Доказательство. При 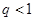 выбираем
выбираем  так, чтобы
так, чтобы  . Пусть
. Пусть  выбрано так, чтобы при
выбрано так, чтобы при 
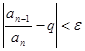 , т.е.
, т.е. 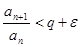 и
и 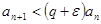 ,
,  . По предыдущей теореме ряд сходится. Если же
. По предыдущей теореме ряд сходится. Если же 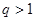 , то выберем
, то выберем  так, что
так, что  . Тогда при
. Тогда при 
 и ряд расходится.
и ряд расходится.
Признаки Коши и Даламбера удобны, но слабоваты. Например, для рядов  и
и  :
:  при
при 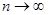 ,
, 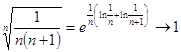 при
при 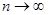 , т.е. признак Коши не применим. Признак Даламбера тем более неприменим, т.к.
, т.е. признак Коши не применим. Признак Даламбера тем более неприменим, т.к. 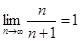 ,
, 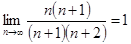 .
.
Однако мы знаем, что гармонический ряд расходится, а для второго ряда легко подсчитать частичную сумму: 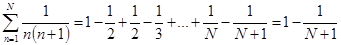 и
и  при
при  . (Здесь использовано тождество
. (Здесь использовано тождество  ), т.е. ряд сходится.
), т.е. ряд сходится.
Теорема. (признак Гаусса). Пусть 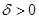 и
и 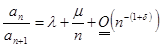 ,
, 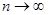 .
.
| Тогда: | Если 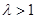 - ряд сходится,
Если - ряд сходится,
Если 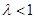 - ряд расходится,
Если - ряд расходится,
Если 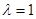 и и  - ряд сходится,
Если - ряд сходится,
Если 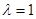 и и 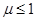 - ряд расходится. - ряд расходится.
|
Эту теорему оставим без доказательства.
В применении к ряду  она дает:
она дает:  ,
, 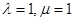 - ряд расходится. Для ряда
- ряд расходится. Для ряда  имеем:
имеем: 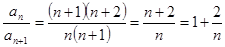 ,
, 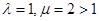 - ряд сходится.
- ряд сходится.
3. Интегральный признак сходимости. Сходимость ряда 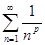
Теорема. Пусть 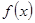 - непрерывная, неотрицательная, монотонно убывающая функция, определенная при
- непрерывная, неотрицательная, монотонно убывающая функция, определенная при 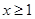 . Тогда ряд
. Тогда ряд  и интеграл
и интеграл  либо оба сходятся, либо оба расходятся.
либо оба сходятся, либо оба расходятся.
Доказательство. Ввиду монотонности при всех  выполняются неравенства
выполняются неравенства  . Интегрируя, получаем
. Интегрируя, получаем  . Тогда
. Тогда 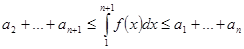 , или
, или 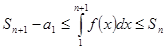 . Поэтому если
. Поэтому если  сходится, то
сходится, то 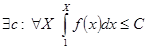 . Тогда
. Тогда 
 и
и  ,
,  ряд сходится.
ряд сходится.
Пусть теперь наоборот, известно, что ряд сходится. Тогда  . Взяв произвольное
. Взяв произвольное 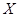 выберем
выберем  так, чтобы
так, чтобы 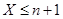 . Тогда
. Тогда  . Значит,
. Значит,  сходится.
сходится.
Геометрическая иллюстрация теоремы.
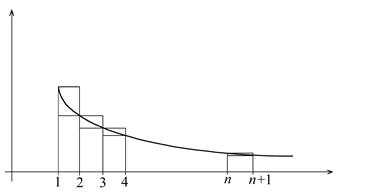
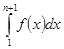 - площадь под графиком
- площадь под графиком 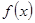 на отрезке от 1 до
на отрезке от 1 до 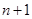 .
.  - площадь “верхней лестницы”, расположенной над графиком и
- площадь “верхней лестницы”, расположенной над графиком и  - площадь “нижней лестницы”, под графиком.
- площадь “нижней лестницы”, под графиком.
Пусть ряд и интеграл сходятся. Тогда остаток ряда  .
.
Теорема. Сходимость ряда 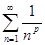 .
.
Ряду 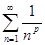 соответствует функция
соответствует функция  .
. 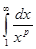 сходится при
сходится при 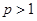 и расходится при
и расходится при 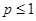 . По доказанной теореме, ряд сходится при
. По доказанной теореме, ряд сходится при 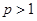 и расходится при
и расходится при 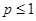 .
.
– Конец работы –
Эта тема принадлежит разделу:
Математический анализ
На сайте allrefs.net читайте: "Математический анализ"
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Доказательство.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов