Модели ARIMA

 

В эконометрике анализ временных рядов с использованием оценки спектральной плотности (спектральный анализ) играет, как правило, вспомогательную роль, помогая установить периоды характерных циклов. Наибольшее распространение получили параметрические модели стационарных случайных процессов – модели авторегрессии и скользящего среднего.

Пусть X_t – значения стационарного случайного процесса, m = EX_t, x_t = X_t -m.. Введем случайный процесс x(t) ÎN(0,s²), для которого Ex_t = 0, Dx_t= s², Ex_tx_t-t= 0 (t¹0). Случайный процесс x_t будем называть белым шумом. В шкале непрерывного времени ему отвечает обобщенный случайный процесс x(t), спектр плотности которого S(τ) = const, при этом корреляционная функция K(τ) = 0 при τ ≠ 0. При τ = 0 корреляционная функция принимает бесконечно большое значение, точнее, K(τ) = s²δ(τ) , где δ(τ) – функция Дирака.

Модель авторегрессии – скользящего среднего (АРСС или ARMA, английское – Auto Regression - Moving Average) имеет вид

x_t+a₁x_t-1+a₂x_t-2 + ….+ a_m x_t-m = ξ_t +b₁ξ _t-1+…+b_n ξ_t-n , (10.1)

числа m и n определяют порядок модели ARMA (m,n). Равенство (10.1) можно записать короче, используя оператор сдвига по времени

Q x_t = x_t-1, Q^s x_t = x_t-s

и операторы-многочлены в (10.1)

a(Q) = 1+a₁Q+ a₂Q²+…+a_mQ^m

b(Q) = 1+b₁Q+b₂Q²+…+b_nQⁿ

В этих обозначениях модель (10.1) запишется в виде

 

a(Q) x_t = b(Q) ξ_t . (10.2)

 

Рассмотрим важные частные случаи. Модель AR(1) авторегрессии I порядка имеет вид

x_t+a₁x_t-1 = ξ_t . (10.3)

Этой дискретной статистической модели соответствует дифференциальное уравнение I порядка в шкале непрерывного времени

.

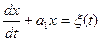Модель AR(2) авторегрессии II порядка имеет вид

x_t+a₁x_t-1+ a₂x_t-2= ξ_t . (10.4)

Её аналогом в непрерывной шкале будет дифференциальное уравнение II порядка

.

Можно показать, что процесс x_t , вычисляемый по дискретной модели (10.3), (10.4),

будет стационарным при условии, что корни функций комплексного переменного

z= x+iy, составленных по правилам φ₁(z) = 1+a₁z для AR(1) и φ₂(z) = 1+a₁z + a₂z² для AR(2), удовлетворяют условию |z| > 1 .

После замены z = 1/ζ получим уравнения

ζ+a₁ = 0; ζ²+b₁ζ+b₂ = 0,

корни которых должны лежать внутри круга единичного радиуса |ζ|<1 (иначе процесс не будет стационарным).

В общем случае модели ARMA (m,n) условие стационарности |z| > 1 должно выполняться для корней функции

При изучении нестационарных временных рядов часто используется более общая модель ARIMA(m,d,n) – модель авторегрессии–проинтегрированного скользящего среднего, в русской аббревиатуре - АРПСС. По сравнению с ранее обсуждавшимися моделями модель ARIMA предполагает d– кратное применение оператора конечных разностей

x_t = y_t - y_t-1 = (1-Q) y_t (10.5)

к исходному временному ряду. Операция (10.5) устраняет линейный тренд. Действительно, если y_t=а+bt, то y_t-1=а+b(t-1) и x_t= b. Повторяя эту операцию несколько раз, можно получить (с некоторым приближением) стационарный временной ряд, который описывает модель ARMA. При восстановлении исходного ряда производится суммирование его членов, что соответствует интегрированию в непрерывном времени. Последнее обстоятельство проясняет смысл названия модели ARIMA.