Расчет погрешностей.

 

Эмпирические данные часто подвергаются математической обработке – над ними

выполняются арифметические операции сложения, вычитания, умножения и деления, в некоторых случаях производится логарифмирование, возведение в степень и др. Как это может сказаться на погрешности результата?

Покажем, что абсолютная погрешность суммы не превосходит суммы абсолютных погрешностей слагаемых. Пусть S=x+y, причем слагаемые x, y известны с абсолютной погрешностью e_x, e_y, так что

,

где a и b – точные значения слагаемых. Для вычисления абсолютной погрешности суммы S оценим разность:

.

Ясно, что в качестве предельной абсолютной погрешности суммы можно принять величину

e_S=e_x+e_y . (14.1)

 

Аналогично проверяется, что абсолютная погрешность разности двух чисел d=x-y равна сумме абсолютных погрешностей уменьшаемого и вычитаемого: e_d=e_x+e_y. Заметим, что если числа x и y мало отличаются между собой, относительная погрешность их разности d_d=e_d / |x-y| может оказаться весьма большой.

При вычислении суммы S=x₁+x₂+…+x_n большого числа слагаемых, имеющих одинаковую абсолютную погрешность e, в соответствии с формулой (14.1) имеем

 

e_S=ne . (14.2)

 

При n>>1 величина e_S может оказаться довольно большой. Но эта оценка получается в

предположении, что ошибки всех слагаемых максимальны и имеют одинаковый знак, что представляется мало вероятным. Более естественным выглядит предположение, что ошибка e является случайной и распределена по нормальному закону 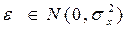, причем ошибки отдельных слагаемых являются независимыми случайными величинами. По правилу вычисления дисперсии сумма независимых случайных величин находим, что: или , так что .

При больших n (например, n=100) статистическая оценка дает значительно меньшее значение, чем предельная (14.2). Напомним, что отклонение случайной величины S от истинного значения более чем на 2s_S возможно с вероятностью 0,045 (4,5%), а на 3s_S – с вероятностью 0,003 или 0,3%.

Для вычисления погрешности произведения и частного двух положительных чисел x, y рассмотрим сначала общий случай функции двух переменных u= f(x,y) (аналогично рассматривается случай функций многих переменных).

Пусть переменная x известна с погрешностью e_x, переменная y – с погрешностью e_y. Приращение функции Du заменим дифференциалом

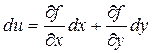, (14.3)

полагая величины e_x и e_y достаточно малыми. Отсюда следует, что абсолютная погрешность e_u функции u оценивается по формуле:

. (14.4)

В статистической теории предполагают ошибки e_x и e_y независимыми случайными величинами. Для дисперсии величины du имеем формулу

. (14.5)

В случае произведения двух положительных чисел u=xy формула (14.4) дает оценку

, (14.6)

а по формуле (14.5) получим

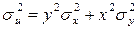. (14.7)

Для относительной погрешности произведения d _u=e _u / xy из формулы (14.6) следует, что

d_u=d_x+d_y , (14.8)

а из формулы (14.7) :

. (14.9)

Пусть надо перемножить n положительных чисел x₁, x₂, …, x_n, заданных с одинаковой относительной погрешностью d. Формула (14.8) дает оценку d_u=nd , а по формуле (14.9) получаем .

Нетрудно убедиться в том, что для относительной погрешности частного U=x/y двух положительных чисел x, y также справедливы формулы (14.8) и (14.9).

Если требуется найти значение функции U=f(x) одной переменной x, то вместо формулы (14.3) имеем (в первом приближении) так что 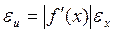. Такой же результат следует из статистического анализа:

.