Принцип максимального правдоподобия. Построение регрессионных моделей при гетероскедастичности ошибок
Для нахождения неизвестных величин по результатам измерений, содержащих случайные погрешности, служит метод наименьших квадратов (МНК). Определяемые величины обычно связаны уравнениями, образующими избыточную систему.
Метод наименьших квадратов строит оценки на основе минимизации суммы квадратов остатков. Для его применения необходимо выполнение следующих пяти условий:
· случайный характер остатков;
· нулевая средняя величина остатков, не зависящих от независимой переменной;
· гомоскедастичность – дисперсия каждого отклонения ei одинакова для всех значений
переменной;
· отсутствие автокорреляции остатков. Значения ei распределены независимо
друг от друга;
· остатки подчиняются нормальному распределению.
Для возможности применения МНК необходимо проверить характер остатков ei по всем пяти условиям.
Если величины ei являются случайными величинами, распределенными по нормальному закону - eiÎN(0,s2), так что Eei = 0, Dei=s2 и некоррелированы -
cov (ei, ej) = 0 (i ¹ j), а значит, и независимы, то можно применить МНК. Постоянство s2
для всех ei означает равноточность задания величины yi; величины xi мы считаем заданными точно. Свойство равноточности измерения yi иначе называется гомоскедастичностью. Если же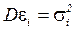 
и si различны, то говорят о гетероскедастичности регрессионной модели.
Пусть эмпирические данные наблюдений (x1, x2, …, xn) характеризуют случайную величину xÎN(m, s2), для которой математическое ожидание m = Ex и дисперсия
s2 = Dx неизвестны и их требуется оценить. Выпишем функции плотности нормального распределения 
. Согласно принципу максимального правдоподобия предполагаем, что функция L=f(x1)f(x2)…f(xn) принимает наибольшее значение при истинных значениях параметров m и s2. Удобнее иметь дело с
.
В нашем примере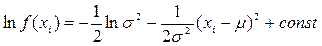 
, поэтому
.
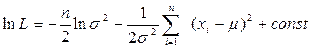Выпишем необходимые условия экстремума функции ln L (и L):
, 
.
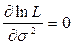Решение этой системы уравнений после простых преобразований приводит к оценкам
,
.
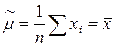Заметим, что
, 
.
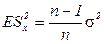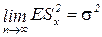Пример показывает, что принцип максимального правдоподобия не обязательно приводит к несмещенной оценке искомых параметров.
Воспользуемся принципом максимального правдоподобия для анализа гетероскедастичности. В этом случае модель парной линейной регрессии имеет вид yi = a+bxi+ei , где Eei = 0, Dei = si2, так что eiÎN(0, si2). Соответствующие плотности вероятностей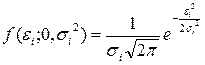 
. Логарифмическая функция правдоподобия
.
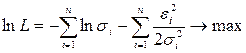Теперь ясно, как модифицировать МНК в случае гетероскедастичности ошибки e i :
.
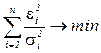В случае гомоскедастичности дисперсии si равны и мы получаем классическую формулировку МНК.
Часто вводится веса наблюдений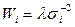 
, при этом число l выбирается так, чтобы веса были целыми числами. МНК сводится к минимизации взвешенных сумм квадратов:
.
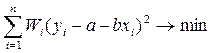