Парная линейная регрессия. Метод наименьших квадратов

 

Пусть имеется n пар чисел (x_i, y_i), i=1,2,…,n, относительно которых предполагается, что они отвечают линейной зависимости между величинами x и y:

y=a+bx, (3.1)

возможно, с некоторой ошибкой e_i, так что

y_i=a+bx_i+e _i, i=1,2,…,n . (3.2)

Какими должны быть наилучшие значения параметров a и b?

Применяя метод наименьших квадратов, мы требуем, чтобы сумма квадратов ошибок e_i была наименьшей:

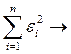min. (3.3)

Подставляя значения e _i из (3.2) в (3.3), получим функцию

min.

Необходимым условием минимума этой функции, как известно, является равенство нулю ее частных производных по a и b:
, .
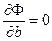Вычисляя производные, приходим к системе уравнений

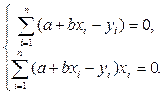(3.4) Заметим, что уравнения (3.4) можно записать короче в виде

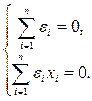(3.5)

Если раскрыть скобки в уравнениях (3.4), то после простых преобразований получим систему

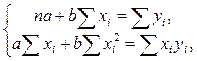(3.6)
решение которой находится без большого труда:

, (3.7)

. (3.8)

Введем обозначения:

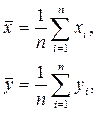(3.9)

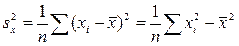, (3.10)

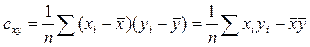. (3.11)

В курсах математической статистики величины 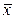,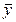называются выборочными средними, ­­­­­­­­ – выборочной дисперсией, 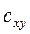– выборочной ковариацией. Теперь формулу (3.8) можно переписать в виде

, (3.12)

а выражение для a получается из первого уравнения (3.6):

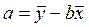. (3.13)

Из формулы (3.13) видно, что точка лежит на прямой y=a+bx (при найденных значениях a и b). Поэтому функцию (3.1) можно записать также в виде 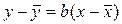, где параметр b определяется по формуле (3.12).

Предположим теперь, что зависимость y от x не является линейной и выражается формулой

y_i = a+bf(x_i)+e_i , i =1,2,…,n . (3.14)

 

Введем обозначения

; , , ,

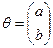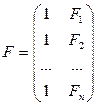где n – число измеренных значений фактора x, а F_i = f(x_i).

В матричной форме система уравнений (3.14) принимает стандартный вид

Y = Fq+e. (3.15)

Для определения параметров a и b, объединенных в вектор q , можно применить метод наименьших квадратов (отметим, что относительно искомых параметров формула (3.14) осталась линейной). В следующем параграфе показано, что решение этой задачи имеет вид

q = (F^TF)^-1F^TY. (3.16)