Множественная линейная регрессия.

 

Парная регрессия может дать хороший результат при моделировании, если влиянием других факторов, воздействующих на объект исследования, можно пренебречь. Но, существует обычно несколько факторов, которые оказывают существенное влияние (например: на потребление того или иного товара влияют такие факторы, как цена товара, размер семьи, её состав, доход и т.д.). В этом случае следует попытаться выявить влияние этих факторов, введя их в модель, т.е. построить уравнение множественной регрессии.

Включение в уравнение множественной регрессии того или иного набора факторов связано прежде всего с представлением о природе взаимосвязи моделируемого показателя с другими экономическими явлениями. Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:

· Факторы должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность. Например, если анализируется спрос на мороженое летом и зимой, то фактор сезонности можно учесть бинарной переменной, принимающей значения 1 и 0. Аналогичным образом учитывается наличие балкона, этаж, тип здания (кирпичный или блочный дом) на рынке недвижимости и т. п.

· Факторы не должны быть коррелированы и тем более находиться в точной функциональной связи.

В случае учета влияния нескольких факторов линейная зависимость величины y от
m переменных x₁, x₂,…, x_m примет вид:

y =q₁x₁+q₂x₂+…+q_mx_m . (4.1)

Конкретные значения независимых переменных будем отмечать двумя индексами: x_i1, x_i2,…, x_im, (i = 1,2,…,n). Тогда можно записать уравнения

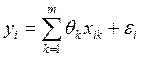, (4.2)

где m – число рассматриваемых факторов.

Зависимость (4.2) будем называть множественной линейной регрессией.

Если зависимость величины y от переменных x₁, x₂,…, x_m имеет вид

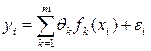, i=1,2,…,n (4.3)

то, введя обозначение F_ik=f_k(x_i), запишем формулу (4.3) в виде

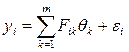. (4.4)

В качестве примеров зависимости типа (4.3) отметим квадратичную функцию y=a+bx+cx² , полином третьей степени y=a+bx+cx² +dx³ , тригонометрический полином y=q ₁ sinx+q₂ sin2x+…+q_m sin mx и др.

Сравнив формулы (4.2) и (4.4), нетрудно убедиться в том, что они отличаются только обозначениями заданных коэффициентов F_ik и x_ik. В матричном виде имеем формулу

 

y=Fq+e , (4.5)

где

, , .

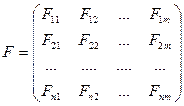Для определения коэффициентов q_k в формулах (4.2) или (4.4) воспользуемся методом наименьших квадратов:

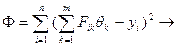min.

Необходимое условие экстремума функции F=F (q₁,q₂,…,q_т)

, p=1,2,…,m

дает уравнение

(4.6)

В уравнении (4.6) переставим порядок суммирования :

(4.7)

В матричной форме система уравнений (4.7) относительно неизвестных значений переменной q_k имеет вид

F^TFq=F^Ty . (4.8)

Полагая, что матрица F^TF неособенная, получим решение системы (4.8)

q=(F^TF)^-1F^Ty . (4.9)

В случае парной регрессии (3.1) вектор параметров q имеет вид

;

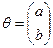переменную x₁ следует принять равной 1, а переменную x₂=x; тогда матрица F принимает вид

.

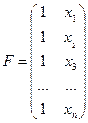Произведение матриц

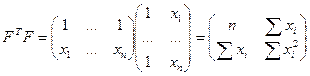
представляет собой матрицу коэффициентов системы (3.6), а свободный член в формуле (4.8)

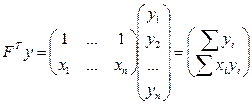
совпадает со свободными членами уравнений (3.6).

Точно также в случае множественной линейной регрессии для уравнения y=q₀+q₁x₁+q₂x₂ первый столбец матрицы F состоит из 1, второй столбец - из заданных значений переменной x₁, а третий – из значений x₂:

;

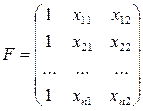Вектор параметров принимает вид

.
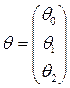