ОЦЕНКА ЛОГИСТИЧЕСКОЙ ФУКЦИИ

 

Логистической кривой иногда пользуются для представления роста населения. В эконометрии ее можно часто рассматривать как тенденцию экономических временных рядов, связанных с населением.

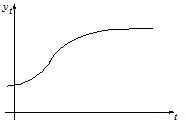
Проще применять тенденцию, состоящую из степеней переменных, выражающих время, или же такую тенденцию, которая являлась показательной функцией относительно времени. Но у таких тенденций неприятное свойство - становиться бесконечными с течением времени. Итак, они, возможно, годяться для интерполяции временных рядов, но вряд ли для их экстраполяций.

И наоборот, логистическая кривая имеет свойство стремиться, при нарастании времени, к асимптоте. Определение логистической функции 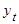будет:

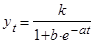(1)

где t - время, k, a, b - постоянные, в общем неизвестные. Постоянная k является верхней асимптотой логистической кривой. Ясно видно, что:

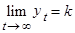(2)

Следовательно k будет наибольшим значением, которое может принять логистическая функция.

Трудности, возникающие при попытке оценить логистическую функцию, хорошо известны. Нужно применять только численные методы, ибо нормальные уравнения, получаемые от применения МНК или максимума вероятностей, не бывают линейными относительно неизвестных параметров.

Гарольд Готелинг, однако, указал на очень интересный метод для оценки этих параметров. Он исходил из дифференциального уравнения логистической функции.

Дифференцируем 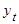в (1). Опуская для краткости подписной значок, имеем первую производную:

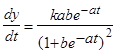
Т.к. согласно (1),

, ,

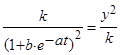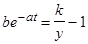то подставляя эти выражения в формулу первой производной, приходим к дифференциальному уравнению:

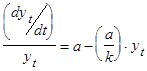(3)

Теперь мы можем применить непосредственно к вышеприведенному дифференциальному уравнению способ наименьших квадратов. Мы сразу же получаем оценочное значение для параметров a и 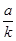, следовательно, и для первоначальных постоянных a и k.

Недостающий параметр b может быть оценен методом Родса:

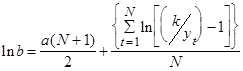(4),

если у нас имеется N наблюдений, происходящих на равных отрезках времени (например ежегодно). В этой функции ln будет натуральным логарифмом (с основанием e).

Но при практическом применении идеи Готелинга встречается следующая трудность: нам нужна норма роста 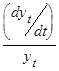, а во всех экономических временных рядах у нас нет непрерывных наблюдений, кроме, например, ежегодных данных.

Логистическая кривая описывается функцией нелинейной по параметрам, подлежащим оценке.

Среднее имеет тенденцию возрастать с убывающей скоростью, а согласно разумным приближением среднего представляется логистическая кривая.

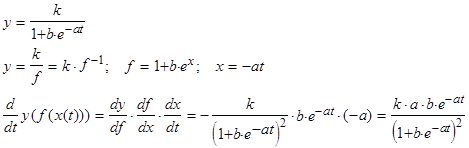
Есть, однако, простой способ преодолеть эту трудность. На один момент посмотрим на логистическую функцию как на закон роста населения. Тогда ее обратное значение пропорционально плотности населения. Отсюда мы имеем простое преобразование:

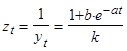(5)

Функция 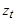имеет линейное разностное уравнение первой степени:

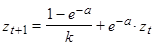(6)

Действительно,

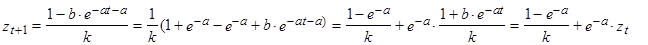
Теперь можно применить к этому разностному уравнению (6) непосредственно метод наименьших квадратов. Мы получим оценочные значения для параметров 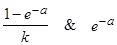, из них можем оценить постоянные а и k логистической функции. Постоянную в можно вычислить затем с помощью формулы Родса (4).

Мы можем применить этот метод для исчисления тенденций роста шведского населения. Имеются следующие данные:

Год	Период	Население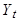
		3 482 541
		3 859 728
		4 168 525
		4 565 668
		4 784 981
		5 135 441
		5 522 403
		5 904 489
		6 142 191
		6 371 432
		7 041 829

Вычисляем обратные значения, т.е. 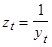, пропорциональные плотности населения.

Методом наименьших квадратов получаем разностное уравнение:

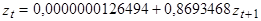(7)

Отсюда получаем оценки:

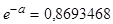и поэтому а=0,14

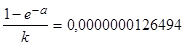и отсюда k=10,328 806

Это верхняя асимптота тенденции шведского народонаселения.

Теперь применим формулу Родса и оценим параметр в: в=2,1176.

Поэтому полная формула для найденной тенденции шведского населения выглядит так:

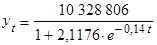(8)

Если теперь подставить в эту формулу t=12, то получим предсказание для численности шведского населения на 1960г. ()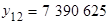

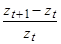
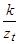
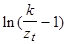
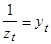
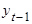
					0,1
		0,3	1,35	- 1,03	0,071	0,1
		0,15	1,17	- 1,77	0,067	0,071
	16,5	0,1	1,07	- 2,66	0,061	0,067
		0,03	1,036	- 3,32	0,059	0,061

Логистическая кривая I способ:

 

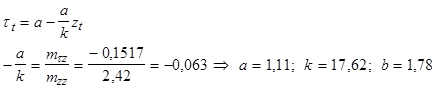
ЛЕКЦИЯ 3.