Законы распределений дискретных случайных величин.

Пусть некоторая СВ является дискретной, т.е. может принимать лишь фиксированные (на некоторой шкале) значения X _i. В этом случае ряд значений вероятностей P(X _i)для всех (i=1…n) допустимых значений этой величины называют её законом распределения.

В самом деле, - такой ряд содержит всю информацию о СВ, это максимум наших знаний о ней. Другое дело, - откуда мы можем получить эту информацию, как найти закон распределения? Попытаемся ответить на этот принципиально важный вопрос, используя уже рассмотренное понятие вероятности.

Точно также, как и для вероятности случайного события, для закона распределения СВ есть только два пути его отыскания. Либо мы строим схему случайного события и находим аналитическое выражение (формулу) вычисления вероятности (возможно, кто–то уже сделал или сделает это за нас!), либо придется использовать эксперимент и по частотам наблюдений делать какие–то предположения (выдвигать гипотезы) о законе распределения.

Заметим, что во втором случае нас будет ожидать новый вопрос, - а какова уверенность в том, что наша гипотеза верна? Какова, выражаясь языком статистики, вероятность ошибки при принятии гипотезы или при её отбрасывании?

Продемонстрируем первый путь отыскания закона распределения.

Пусть важной для нас случайной величиной является целое число, образуемое по следующему правилу: мы трижды бросаем симметричную монетку, выпадение герба считаем числом 1 (в противном случае 0) и после трех бросаний определяем сумму S.

Ясно, что эта сумма может принимать любое значение в диапазоне 0…3, но всё же - каковы вероятности P(S=0), P(S=1), P(S=2), P(S=3); что можно о них сказать, кроме очевидного вывода - их сумма равна 1?

Попробуем построить схему интересующих нас событий. Обозначим через p вероятность получить 1 в любом бросании, а через q=(1–p) вероятность получить 0. Сообразим, что всего комбинаций ровно 8 (или 2³), а поскольку монетка симметрична, то вероятность получить любую комбинацию трех независимых событий (000,001,010…111) одна и та же: q³ = q²·p =…= p³ = 0.125 . Но если p # q , то варианты все тех же восьми комбинаций будут разными:

Таблица 1-1

Первое бросание
Второе бросание
Третье бросание
Сумма S
Вероятность P(S)	q3	q2·p	q2·p	q·p2	q2·p	q·p2	q·p2	p3

 

Запишем то, что уже знаем - сумма вероятностей последней строки должна быть равна единице:

p³ +3·q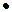p² + 3·q²·p + q³ = (p + q)³ = 1.

Перед нами обычный бином Ньютона 3-й степени, но оказывается - его слагаемые четко определяют вероятности значений случайной величины S !

Мы “открыли” закон распределения СВ, образуемой суммированием результатов n последовательных наблюдений, в каждом из которых может появиться либо 1 (с вероятностью p), либо 0 (с вероятностью 1– p).

Итог этого открытия достаточно скромен:

· возможны всего N = 2 ⁿ вариантов значений суммы;

· вероятности каждого из вариантов определяются элементами разложения по

степеням бинома (p + q) ⁿ ;

· такому распределению можно дать специальное название - биномиальное.

Конечно же, мы опоздали со своим открытием лет на 300, но, тем не менее, попытка отыскания закона распределения с помощью построения схемы событий оказалась вполне успешной.

В общем случае биномиальный закон распределения позволяет найти вероятность события S = k в виде

P(S=k)=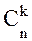·p^k·(1– p)^n-k, {2–1} где 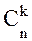- т.н. биномиальные коэффициенты, отыскиваемые из известного “треугольника Паскаля” или по правилам комбинаторики - как число возможных сочетаний из n элементов по k штук в каждом:

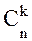= n·(n –1)· ...·(n – k + 1)/ (1·2· .... · k). {2–2}

Многие дискретные СВ позволяют построить схему событий для вычисления вероятности каждого из допустимых для данной случайной величины значений.

Конечно же, для каждого из таких, часто называемых "классическими", распределений уже давно эта работа проделана ­– широко известными и очень часто используемыми в прикладной статистике являются биномиальное и полиномиальное распределения, геометрическое и гипергеометрическое, распределение Паскаля и Пуассона и многие другие.

Для почти всех классических распределений немедленно строились и публиковались специальные статистические таблицы, уточняемые по мере увеличения точности расчетов. Без использования многих томов этих таблиц, без обучения правилам пользования ими последние два столетия практическое использование статистики было невозможно.

Сегодня положение изменилось – нет нужды хранить данные расчетов по формулам (как бы последние не были сложны!), время на использование закона распределения для практики сведено к минутам, а то и секундам.

Уже сейчас существует достаточное количество разнообразных пакетов прикладных компьютерных программ для этих целей. Кроме того, создание программы для работы с некоторым оригинальным, не описанным в классике распределением не представляет серьезных трудностей для программиста “средней руки”.

Приведем примеры нескольких распределений для дискретных СВ с описанием схемы событий и формулами вычисления вероятностей. Для удобства и наглядности будем полагать, что нам известна величина p – вероятность того, что вошедший в магазин посетитель окажется покупателем и обозначая (1– p) = q.

 

· Биномиальное распределение

Если X – число покупателей из общего числа n посетителей, то вероятность P(X= k) = 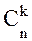·p^k·q^n-k .

· Отрицательное биномиальное распределение (распределение Паскаля)

Пусть Y – число посетителей, достаточное для того, чтобы k из них оказались покупателями. Тогда вероятность того, что n–й посетитель окажется k–м покупателем составит P(Y=n)=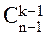·p^k ·q^n–k.

· Геометрическое распределение

Если Y – число посетителей, достаточное для того, чтобы один из них оказался

покупателем, то P(Y=1)= p ·q^n–1.

· Распределение Пуассона

Если ваш магазин посещают довольно часто, но при этом весьма редко делают покупки, то вероятность k покупок в течение большого интервала времени, (например, – дня) составит P(Z=k) = l^k ·Exp(-l) / k! , где l – особый показатель распределения, так называемый его параметр.