Эквивалентность функций.

d - отношение эквивалентности

Df: Пусть D - множество диф-мых на промежутке I функций F d G <=> F' = G'

Df: Введем понятие отношения t: F t G <=> F - G = const

Th: t совпадает с d

Доказательство:

а) F t G => по определению => F - G = const => (F - G)' = 0 => F'=G' => F d G

б) F экв G => F' = G', H(х) = F(x) - G(x), H(х)' = 0

Применим теорему Лагранжа

Возьмем x₀ Î I=[a,b] по условию F и G дифференцируемы на I => H - диф-ма на I

H(х) - H(х₀) / x - x₀ = H(s)' x₀ < s < x

H(х)-H(х₀) = (x-x₀) * H(s)'

H(х)-H(х₀) = (x-x₀) * 0

H(х)=H(х₀) => H(х) = F(x) - G(x) - const => F t G

Df: Возьмем функцию FÎD[F]_d=[F]_t=òf(x)dx - н/о интеграл f(x), где f(x)=F'(x). Пусть С - мн-во всех ф-ций с пост. значением, тогда: òf(x)dx=F+C={F+с |сÎR}

Простейшие свойства:

a(F + С) = aF + С, a нельзя перед С так как при a = 0 некорректность

(F + С)+ (G + С) = F + G + С, здесь С = 2С = ... = aС

1) aòf(х)dx = òaf(х)dx

2) ò(f(х) + g(х))dx = òf(х)dx + òg(х)dx

3) òf(х)`dx = f(х) + C

4) (òf(х)dx)` = f(х) (dòf(x)dx = f(x)dx)

Таблица интегралов:

1) òх^mdx = x^m+1/ m+1 + C (m ¹ -1)	7) ò1 / cos²x dx = tgx + C
2) ò1 / 1+x²dx = arctgx + C = -arcctgx + C	8) ò1 / sin²x dx = -ctgx + C
3) ò1 / Ö(1-x²)dx = arcsinx + C = -arccosx + C	9) ò1/x dx = ln\|x\| + C
4) òa^xdx = a^x/ lna + C	10) òe^xdx = e^x + C
5) òsinxdx = -cosx + C; òcosxdx = sinx + C	11) ò1 / 1-x²dx = ln\|1+x / 1-x\| + C

2. Подстановка и замена переменной в н/о интеграле

Th: Пусть 1) òf(x)dx = F(x)+C на I; 2) g Î D g: J®I, тогда òf(g(t))g'(t)dt = F(g(t))+C

Доказательство: Из условия (1) F(x) на I непрерывна, из (2) g(t) непрерывна на I => функция F(g(t)) - непрерывна на I => имеем право продифференцировать, учитывая что F'(x)=f(x) (1) по правилу диф-ния сложных функций получаем: F`(g(t)) = f(g(t))g'(t) => функция f(g(t))g'(t) одной из своих первообразных имеет функцию F(g(t)) => $f(g(t))g'(t)dt = F(g(t)) + C

Th: Замена переменной: Пусть 1) òf(v(t))v'(t)dt = F(t) + C на I;

2) v: I®J u: J®I u = v ^-1;

3) t = u(x).

Тогда òf(x)dx = F(u(x)) + C на J

Доказательство: f(v(t)) = f(v(u(x))) = f(x). v'(u(x))du(x) = v'(u(x))u'(x)dx = dx (по теореме о производной обратной ф-ции).Подставив в (1), получим то, что надо.

3. Интегрирование по частям

Th: Пусть u & v дифференцируемы на I и существуют интегралы, тогда òu(x)v`(x)dx = u(x)v(x) - òu'(x)v(x)dx

Доказательство:

Þ Пусть F Î uv - òu'vdx => F' = (uv - òu'vdx)' = u'v + v'u - u'v = v'u => F Î $uv'dx

Ü Пусть F Î òuv'dx докажем что F Î uv - u'vdx или то, что (uv - F) Î òu'vdx для этого продиференцируем (uv - F): (uv - F)' = u'v+v'u-uv' = u'v => (uv - F) Î òu'vdx.

7.Интегралы вида òR(x,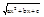dx) a ¹ 0

Такой интеграл приводится к интегралу от рациональной функции нового переменного c помощью подстановок Эйлера:

1) Первый случай: a > 0

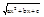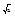= ± x± t

Возведем обе части в квадрат: ax²+bx+c=ax²±2xt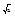+t², отсюда:

x=t²-c/b±2t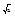= R₁(t) - рациональная функция.

dx = R₁'(t)dt, R₁'(t) тоже Î R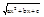[x]:= ±x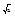±t = ±R₁(t)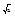±t = R₂(t), т.о. òR(x, sqr(ax²+bx+c)dx = òR(R₁(t), R₂(t))R₁'(t)dt

2) Второй случай: Корни трехчлена ax²+bx+c - действительны. Пусть x₁, x₂ - корни трехчлена ax²+bx+c

a) x₁=x₂ =>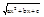==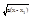 |x-x₁|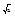

если a < 0 то при x ¹ x₁ под корнем стоит мнимая величина и этот случай нет смысла рассматривать

если a > 0 то после указанного преобразование получаем, что переменная x не входит под знак корня, т.е. под интегралом стоит просто рациональная функция от x, вообще говоря разная для каждого из промежутков (-¥,x₁) и (x₁,+¥)

б) x₁ ¹ x₂=>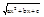= |x-x₁|

Получаем: òR(x,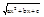)dx = òR(x,|x-x₁|)dx = R₃(x,) - этот интеграл сводится к интегралу от рациональных функций как частный случай интеграла вида: òR(x,(ax+b/cx+d)^m1,...,(ax+b/cx+d)^mk)dx

3) c > 0

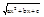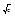= ±±xt

ax²+bx+c = c ±2xt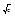+ x²t²

x = b±2t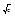/t²-a = R₄(t)

dx = dR₄(t) = R₄'(t)dt

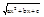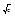= ±±xt = ±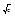± R₄(t)t = R₅(t), где R₄(t), R₄'(t), R₅(t) - суть рациональные функции, поэтому R(x, sqr(ax² +bx +c)dx = òR(R₄(t),R₅(t))R₄'(t)dt = òR_R (t)dt, где R_R(t) - рациональная функция.

Иногда кроме подстановок Эйлера применяют тригонометрические и гиперболические подстановки.