Замена переменной в определенном интеграле и интегрирование по частям.
Замена переменной в определенном интеграле и интегрирование по частям. - раздел Математика, Первообразная, разбиение их множества на классы и определение интеграла. Таблица интегралов. Теорема О Замене Переменной: Пусть G Монотонна На [A,b] И G’...
Теорема о замене переменной: Пусть g монотонна на [a,b] и g’ Î C[a,b], f Î C[g(a),g(b)], тогда
Доказательство: F(x) Î òf(x)dx => F(g(t)) Î òf(g(t))g’(t)dt
Теорема об интегрировании по частям: Пусть u,v Î C[a,b], тогда
Доказательство: F Î òuv'dx, G ÎР òu'vdx; F + G = uv + C;
20.Приближенное вычисление интегралов: формула прямоугольников.
h = b-a / n
mi = xi + h/2
sN = n(f(xо +h/2) + f(x1 +h/2) +...+f(xN-1 +h/2))
c - середина любого из промежутков
f(x) = f(c) + f’(c)(x-c) + f’’(q)(x-c)2 / 2, q Î [c-h/2, c+h/2]
R = m/2 *
N +
22.Приближенное вычисление интегралов: формула Симпсона
Рассмотрим интеграл на промежутке [-1,1] от функции f(x): f(x) Î R, degf £ 2.
– Конец работы –
Эта тема принадлежит разделу:
На сайте allrefs.net читайте: Первообразная, разбиение их множества на классы и определение интеграла. Таблица интегралов....
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ:
Замена переменной в определенном интеграле и интегрирование по частям.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
Все темы данного раздела:
Эквивалентность функций.
Интегрирование дробно-рациональных функций (случай простых корней)
Интегрирование дробно-рациональных функций (случай кратных корней)
Интегрируемость по Риману. Ограниченность итегрируемой функции.
Суммы Дарбу и их свойства
Критерий интегрируемости
Интегрируемость непрерывных и монотонных функций.
Среднее значение функции на отрезке.
И дифференцируемость. Существование первообразной у непрерывной функции.
Формула Ньютона-Лейбница
Сходимость несобственного интеграла и ряда. Их взаимосвязь. Критерий Коши.
Абсолютная и условная сходимости. Теоремы сравнения.
Интегральный признак сходимости ряда.
Ряды Лейбница
Степенные ряды. Область сходимости.Радиус сходимости и его вычисление.
Открытые, замкнутые, компактные множества. Фундаментальные последовательности на компакте.
Предел и непрерывность функции многих переменных. Свойства непрерывной функции на компакте.
Связанные множества. Теорема о промежуточном значении.
Дифференцируемость. Производные по направлению.
Поверхности уровня. Касательная плоскость.
 =
= 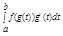
 = F(g(b))- F(g(a));
= F(g(b))- F(g(a)); 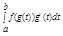 = F(g(b))- F(g(a)) =>
= F(g(b))- F(g(a)) =>  = F(g(b))- F(g(a)) =
= F(g(b))- F(g(a)) =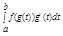
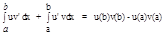
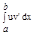 = F(b) - F(a);
= F(b) - F(a); 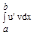 = G(b) - G(a)
= G(b) - G(a)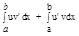 = F(b)-F(a)+G(b)-G(a) = F(b)+G(b)-(F(a)+ G (a)) = (u(b)v(b)+C) - (u(a)v(a) + C) = u(b)v(b) - (u(a)v(a)
= F(b)-F(a)+G(b)-G(a) = F(b)+G(b)-(F(a)+ G (a)) = (u(b)v(b)+C) - (u(a)v(a) + C) = u(b)v(b) - (u(a)v(a)
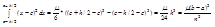 , где inf f'' £ m £ sup f''
, где inf f'' £ m £ sup f'' =>
=> 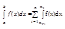 = sN +
= sN +

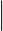
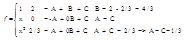
 = 1/3[f(-1) + 4f(0) + f(1)]
= 1/3[f(-1) + 4f(0) + f(1)]

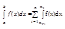 =
= [f(a) + 4f(a + h/2) + 2f(a + h) + 4f(a + 3/2h) + 2f(a + 2h) + +...+ 2f(b-h) + 4f(b-h/2) + f(b)] +
[f(a) + 4f(a + h/2) + 2f(a + h) + 4f(a + 3/2h) + 2f(a + 2h) + +...+ 2f(b-h) + 4f(b-h/2) + f(b)] +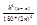 - формула Симпсона
- формула Симпсона






Новости и инфо для студентов