Замена переменной в определенном интеграле и интегрирование по частям.

Теорема о замене переменной: Пусть g монотонна на [a,b] и g’ Î C[a,b], f Î C[g(a),g(b)], тогда =

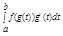
Доказательство: F(x) Î òf(x)dx => F(g(t)) Î òf(g(t))g’(t)dt

= F(g(b))- F(g(a)); = F(g(b))- F(g(a)) 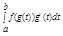=> = F(g(b))- F(g(a)) =

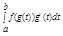
Теорема об интегрировании по частям:Пусть u,v Î C[a,b], тогда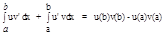

Доказательство: F Î òuv'dx, G ÎР òu'vdx; F + G = uv + C; 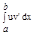= F(b) - F(a); 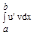= G(b) - G(a)

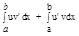= F(b)-F(a)+G(b)-G(a) = F(b)+G(b)-(F(a)+ G (a)) = (u(b)v(b)+C) - (u(a)v(a) + C) = u(b)v(b) - (u(a)v(a)

 

20.Приближенное вычисление интегралов: формула прямоугольников.

h = b-a / n

m_i = x_i + h/2

s_N = n(f(x_о+h/2) + f(x₁+h/2) +...+f(x_N-1+h/2))

c - середина любого из промежутков

f(x) = f(c) + f’(c)(x-c) + f’’(q)(x-c)² / 2, q Î [c-h/2, c+h/2]

R = m/2 *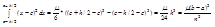, где inf f'' £ m £ sup f''

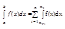=> = s_N +

 

22.Приближенное вычисление интегралов: формула Симпсона

Рассмотрим интеграл на промежутке [-1,1] от функции f(x): f(x) Î R, degf £ 2.

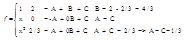
= 1/3[f(-1) + 4f(0) + f(1)]

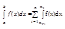=[f(a) + 4f(a + h/2) + 2f(a + h) + 4f(a + 3/2h) + 2f(a + 2h) + +...+ 2f(b-h) + 4f(b-h/2) + f(b)] +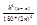- формула Симпсона