Сходимость несобственного интеграла и ряда. Их взаимосвязь. Критерий Коши.

[a,b) b Î RÇ{¥} " b' < b f(x) Î L[a,b`] => F(x) = (a£x£b)

Df: сходится если $ lim F(x), в случае существования предела = lim f(x) при x®b-

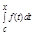Замечание: Пусть c Î [a,b), тогдасходится <=> сходится. = +

 

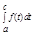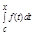
Критерий Коши: сходится <=> " E>0 $ b' Î [a,b): " x₁, x₂ Î (b`,b) ||<E

в точке b - особенность (b=¥ или в точке b подинтегральная функция неопределена)

"=>" lim = A

По определению: " E>0 $ b' Î [a,b): "x Î (b',b) |-A| < E

x₁, x₂ Î (b',b) |- A | < E/2; |- A | < E/2; =>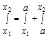

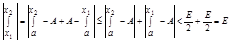
"<=" " E>0 $ b' Î [a,b): " x₁,x₂ Î (b',b) => 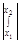< E

Возьмем произвольную последовательность x_N Î [a,b) x_N®b-. A_N =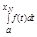- последовательность, надо показать, что она сходится => достаточно доказать фундаментальность.E>0 (b',b) $ n₀: n>n₀ => x_N Î (b',b) => при n>n₀ p>0<E

== |A_N+P - A_N| < E - это определение фундаментальности последовательности A_N

Ряд: S_0...¥a_K = limS_1...N a_K при n®¥

S_1...N a_K - частичная сумма ряда

Критерий Коши сходимости ряда:

S_0...¥ a_K - сходится <=> " E>0 $ n₀: " n>n₀ " p>0 |a_N+1 + ... + a_N+P|<E

Доказательство:

S_0...¥ a_K - сходится <=> $ lim S_0...N a_K <=> последовательность А_N = S_0...N a_K фундаментальна <=> " E>0 $ n₀: " n>n₀ " p>0

E>|a_N+1 + ... + a_N+P| = |A_N+P -A_N| => А_N фундаментальна

Следствие: (необходимый признак сходимости):

Если S_0...¥ a_K сходится, то " p>0 lim (a_N+1+...+ a_N+P) = 0 при n®¥

Доказательство: по критерию фиксируем p раньше выбора номера и видим, что |a_N+1+...+ a_N+P| < E => lim(a_N+1 +...+ a_N+P) = 0 при n®¥

Th:(связь несобственного интеграла с ряда):

сходится <=> " x_N®b-: x_N³a ряд S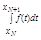сходится.

Доказательство:

"=>" Пусть x_N ³ a, x_N®b-, интеграл сходится => $ lim =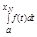

S_0...N-1= 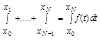- сходится, т.к.=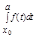(константа) +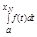(сходится см выше)

"<=" x₀ = a x_N®b- S_0...N - ряд сходится

$ lim S_0...N = lim 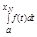= сумма ряда