Абсолютная и условная сходимости. Теоремы сравнения.
У всех интегралов в b особенность
Df:
сходится абсолютно если 
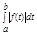сходится => S0...¥aK сходится абсолютно если S0...¥|aK| - сходится
Th: Абсолютно сходящийся интеграл (ряд) сходится.
Доказательство:
=> 
|
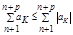Согласно критерию Коши: для интеграла: " E>0 $ b' x1,x2 Î (b',b) => 
=>
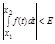
Согласно критерию Коши: для ряда: " E>0 $ n0: " n>n0 " p>0 |aN+1| + ... + |aN+P| < E =>
|aN+1 + ... + aN+P| £ |aN+1| + ... + |aN+P| < E т.е.|aN+1 + ... + aN+P| < E
Признак сравнения 1:a) Пусть 0 £ f(t) £ g(t) при t Î [a,b] и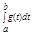 
сходится, тогда - сходится
б) 0 £ aK £ bK k Î Z+ и S0...¥ bK cходится, тогда S0...¥aK cходится.
Доказательство:
a) G(x) =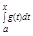 
; F(x) = 
G(x) монотонно растет, F(x) - монотонно растет, берем xN®¥, F(xN) - монотонно растет £ G(xN) - монотонно растет
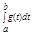®=> F(xN) - ограничена сверху числом => F(xn) сходится
б) аналогично
Признак сравнения 2:B = S0...¥ bK, A = S0...¥ aK, если существует предел lim aN/bN = K, тогда
a) если ряд B сходится и 0 £ k < +¥, то ряд A также сходится
б) если ряд B расходится и 0 < k £ +¥, то ряд A также расходится
Доказательство:
a) по определению предела aN/bN < K + E => aN < bN * (K + E). Так как ряд B сходится => ряд C = S0...¥ (K + E) bK - также сходится => aN < bN *(K + E) => S0...¥ aK < S0...¥ (K + E) bK => по признаку сравнения 1, что ряд A сходится.
б) по свойствам пределов при K>0 $ предел отношения aN/bN => A должен расходится иначе по доказанному в a) B также сходится, что противоречит условию.
Признак сравнения 3: B = S0...¥bK, A = S0...¥aK Если $ n0: " n>n0 выполняется неравенство: aN+1/aN £ bN+1/bN, тогда из сходимости ряда B вытекает сходимость ряда A, а из расходимости ряда A вытекает расходимость ряда B.
Доказательство: Отбросим члены до n0 и перенумеровав их (n0, n1, n2...) получим: a2/a1 £ b2/b1, a3/a2 £ b3/b2,...,aN/aN-1 £ bN/bN-1
Перемножив почленно эти неравенства получим: aN/a1 £ bN/b1 => aN £ bNa1/b1, так как aNb1/a1 £ bN
Пусть ряд B сходится => сходится ряд C = S0...¥ bK a1/b1 => по первому признаку сравнения сходится ряд A.
Пусть ряд A расходится => расходится ряд D = S0...¥ aK b1/a1 => расходится ряд B, так как иначе по первому признаку сходимости сходился бы ряд D - противоречие.
25.Признаки сходимости Д'Аламбера и Коши
Признак Д'Аламбера: Пусть aN®0 и lim aN+1/aN = w при n®+¥ (w Î RÈ{+¥}, тогда
1) если w>1, то S0...¥ aN - расходится
2) если w<1, то S0...¥ aN - сходится
Доказательствво:
1) lim aN+1/aN > 1 => $ n0: " n>n0 aN+1 > aN => lim aN ¹ 0 => нарушено необходимое условие сходимости ряда (следствие из критерия
сходимости рядов Коши) => ряд расходится
2) w < 1, w’ = w+E, w’ Î (w,1)
Рассмотрим aN+1/aN £ w < w’: $ n0: " n ³ n0
aNo+1/aNo * aNo+2/aNo+1 *...* aNo+K/aNo+K-1 = aNo+K/aNo < (w')K
aNo+K < aNow’KaNow’K - ряд S0....¥ aNow’K сходится как бесконечно убывающая геометрическая прогрессия со знаменателем w’ => сходится ряд S0...¥ aNo+K => сходится ряд S0....¥ aNk = S0...¥ aNo+K + S0...No aNo+K (константа)
Признак Коши: Пусть aN > 0 и lim aN1/N = q, тогда
1) если q > 1 => S0...¥ aN - расходится
2) если q < 1, то S0...¥ aN - сходится
Доказательство:
1) aN1/N ® q >1 => $ k0: " k ³ k0 aNk1/Nk >1 => aNk > 1 - бесконечно много членов ряда >1 => lim aN ¹ 0 => ряд расходится
2) q <1, lim aN1/N = q q < q' < 1
В интервале (q',1) не может быть бесконечно много членов последовательности aN1/N (так как тогда в эпсилон окрестности точки q (E < (q+q')/2) находится конечное число членов последовательностити - противоречие так как q - предел aN1/N) => $ n ³ n0: aN1/N £ q' => aN £ q'N => S0...¥ aN £ S0...¥ q'N, S0...¥ q'N - сходится как бесконечно убывающая геометрическая прогрессия => по первому признаку сравнения S0...¥ aN - также сходится.