Интегрирование дробно-рациональных функций (случай простых корней)

P(x)/Q(x) - др/рац. функция над полем R, degP(x)<degQ(x) => дробь правильная.

Если дробь неправильная => P = Q*q+r, P/Q = q+r/Q, где r/Q - правильная дробь

Лемма: Сумма правильных дробей - правильная дробь (если сумма ¹ 0).

Доказательство: P₁/Q₁ + P₂/Q₂ = P₁Q₂+P₂Q₁ / Q₁Q₂

degP₁ < degQ₁ ³ degP₁Q₂ < degQ₁Q₂

degP₂ < degQ₂ ³ degP₂Q₁ < degQ₂Q₁

deg(P₁Q₂+P₂Q₁) £ deg[max(P₁Q₂,P₂Q₁)] < degQ₂Q₁

Интегрирование дробей вида: 1/(x-l)^k, 1/x²+px+q, Ax+B/x²+px+q

1)

a² = q - p²/4 > 0 => дискриминант (x²+px+q) < 0 b=x + p/2 c = b/a

2)

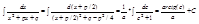
3)

P(x)/Q(x) - правильная дробь (Q(x) - без кратных корней)

z₁, z₂, z₃, ...,z_n Î полю комплексных чисел

Th: Пусть P(x) & Q(x) - многочлены над полем комплексных чисел

degP(x) < n Q(x)=(x-z₁)(x-z₂)(x-z₃)...(x-z_n) z_i ¹ z_j при i ¹ j

Тогда $ ! A₁...A_N Î C: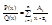

Доказательство: Пусть такие A₁...A_N существуют докажем их единственность:

P(x)=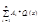, где

P(x_i)=A_i*Q_i(x_i) A_I =P(x_i) / Q_i(x_i) - единственность очевидна

Теперь возьмем A₁...A_N такие, что A_i=P(x_i)/Q_i(x_i) и докажем, что они удовлетворяют условию теоремы.

Доказательство от противного:

Пусть A₁...A_N такие, что A_j = P(x_i) / Q_j(x_i) не удовлетворяют условию теоремы => P(x) - 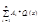= R(x), R(x) ¹ 0 degR(x) £ n-1

R(z_j) = P(z_j) - = P(z_j) - A_JQ_J(z_j) (так как A_IQ_I(z_j) = 0 при i ¹ j)

R(z_j) - P(z_j) + A_JQ_J(z_j) = 0. Так как degR(x) < n, degP(x) < n, degQ_J(x) < n => degR(x) - P(x) + A_JQ_J(x) < n, но у многочлена R(x) - P(x) + A_JQ_J(x) не меньше n корней (z₁,...,z_n - корни) => противоречие.

Следствие: Пусть P и Q Î R[x], Q(x)=(x-z₁)(x-z₂)(x-z₃)...(x-z_s)(x²+xp₁+q₁)(x²+xp₂+q₂)...(x²+xp_k+q_k), где s - число действительных корней, k - число попарно сопряженных корней, причем Q не имеет кратных корней, тогда $ A₁...A_S, B₁...B_K, C₁...C_K Î R такие что:

P/Q = A₁ / x-z₁+...+A_S / x-z_s + B₁x+C₁ / (x²+xp₁+q₁)+...+B_Kx+C_K / (x²+xp_k+q_k)

w_i и w_i' - комплексные попарно сопряженные корни уравнения x²+xp_i+q_i =>

Q(x)=(x-z₁)(x-z₂)(x-z₃)...(x-z_s)(x-w₁)(x-w_1')...(x-w_k)(x-w_k') => по теореме получаем:

P/Q = A₁/x-z₁+...+A_S/x-z_s + E₁/x-w₁ + F₁/x-w_1' + ... + E_K/x-w_k + F_K/x-w_k'

Сопряжем полученное выражение:

P' = P, Q' = Q, z_i' = z_i

P/Q = A_1'/x-z₁+...+A_S'/x-z_s + E_1'/x-w_1'+ F_1'/x-w₁ + ... + E_K'/x-w_k + F_K'/x-w_k

Из единственности разложения (по теореме) получаем:

A_I'=A_I, i=1,...,s => A_I Î R

E_J = F`_J, j=1,...,k

E_J/x-w_j + F_J/x-w'_j = (E_J + F_J)x - (F_J * w_j + E_J * w'_j) / (x²+xp_j+q_j) =

(F`<sub>J</sub>+F<sub>J</sub>)x-(F<sub>J</sub>*w<sub>j</sub>+F`_J*w'_j)/(x²+xp_j+q_j)=(F`_J+ F_j)x-((F_J*w_j)+(F_J*w_j)')/(x²+xpj+qj)

(F`_J + F_J) = B Î R

(F_J * w_j) + (F_J * w_j)' = C Î R

9. Интегралы вида òR(sinx,cosx)dx

Подстановка: u = tg x/2 -П < x < П

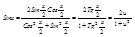
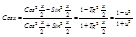
x = ò2arctg u, dx = 2du / 1+u²

Отсюда R(sinx,cosx)dx=òR(2u/1+u²,1-u²/1+u²)2du/1+u²-интеграл от рац-ных функций.

8. Интегралы вида òx^m(a+bxⁿ)^pdx

Замена: x = t^1/n => dx = 1/n * t^{1/n - 1}dt и òx^m(a+bxⁿ)^pdx = 1/n * ò(a+bt)^p*t^{(m+1/n - 1)}dt

Т.о., интеграл òx^m(a+bxⁿ)^pdx сводится подстановкой x=t^1/n к интегралу типа: ò(a+bt)^p*t^qdt, где p и q рациональны, q = m+1 / n-1

1 случай) p - целое число.

Пусть q = r/s, где r,s - целые числа, в таком случае подстановка z = t^1/s (t=z^s) сводит исходный интеграл к интегралу от рациональной дроби: dt = sz^(s-1)dz => ò(a+bt)^p*z^r * sz^(s-1)dz = sò(a+bt)^p*z^(r+s-1)dz

2 случай) q - целое

Пусть p = r/s, где r,s - целые числа, в таком случае подстановка z = (a + bt)^1/s сводит исходный интеграл к интегралу от рациональной дроби: t = (z^s - a) / b => dt = (1/b * sz^s-1)dz => òz^r * ((z^s - a) / b)^q * (1/b * sz^s-1)dz = ò(z^s - a) / b)^q * s/b * z^(r+s-1)

3 случай) p+q - целое

Пусть p = r/s r и s целые. ò(a+bt)^p*t^qdt = ò((a+bt)/t)^p*t^(q+p)dt, в таком случае подстановка z=((a+bt)/t)^1/s сводит исходный интеграл к интегралу от рац. дроби: t=a/(z^s-b) =>

dt = -asz^(s-1)/(z^s-b)² => ò((a+bt)/t)^p*t^(q+p)*-asz^(s-1)/(z^s-b)² = -a^(q+p+1)sòz^(r+s-1)/(z^s- b)^q+p+2