Интегрирование дробно-рациональных функций (случай кратных корней)

Лемма1: Пусть P(x), Q(x) над полем R[x] degP(x)<degQ(x); Q(x)=(x-z)^kR(x) k³2, R(z)¹0, тогда $AÎR и P'(x) над R[x]: òP(x)/Q(x)dx=A/(x-z)^k-1+òP'(x)dx/R(x)(x-z)^k-1.

Доказательство: Сначала из существования P'(x) докажем что такое А существует и определяется однозначно. Дробь под интегралом правильная (так слева и в сумме справа все дроби правильные) все коэффициенты и многочлены опр. единственным образом Продифференцируем обе части равенства: P(x)/Q(x)=A(1-k)/(x-z)^k+P'(x)/R(x)(x-z)^k-1, поскольку Q(x)=(x-z)^kR(x) получаем: P(x) = A(1-k)R(x) + P'(x)(x-z), P(z) = A(1-k)R(z), R(z)¹0 => Отсюда А определяется однозначно.

Теперь возьмем такое А и проверим найдется ли многочлен

P'(x): P(z) - A(1-k)R(z) = 0 => по теореме Безу P(z) - A(1-k)R(z) = (x-z)P'(x)

Лемма 2: Пусть Q(x)=R(x)(x²+px+q)^k, k³2, zz' = q, z + z' = -p, R(z) ¹ 0, тогда $ A,BÎR и P'(x)ÎR[x]: òP(x)/Q(x)dx=Ax+B/(x²+px+q)^k-1 + òP'(x)dx/R(x)(x² + px +q)^k-1

Доказательство: Сначала из существования P'(x) докажем что такие А и B существуют среди действительных чисел и определяются однозначно. Дробь под интегралом правильная (так слева и в сумме справа все дроби правильные) все коэффициенты и многочлены определяются единственным образом Продифференцируем обе части равенства:

, учитывая что Q(x) = R(x)(x²+px+q)^k получаем:

P(x) = A(x²+px+q)R(x) + (Ax+B)(1-k)(2x+p)R(x) + P'(x)(x²+px+q)

P(z) = (Az+B)(1-k)(2z+p)R(z) - остальное в ноль при x=z

(1-k)(2z+p)R(z) ¹ 0 (используем условие => R(z) & (1-k) ¹ 0, 2z - комплексное, а p - действительное число => 2z-p ¹ 0) => Az+B - определяется однозначно Az+B = c Î C если вместо z подставить z' получим: Az' + B = c' (так как в исходном заменили все переменные на сопряженные => получим сопряженное первому результату число)

{ Az + B = c

{ Az' + B = c'

A = (c- c') / (z - z') = 2Imc/2Imz = Imc/Imz => A Î R

{ B = c - Az

{ B = c'- Az'

B = (c' + c) - 2A*(z'+z) = Rec - 2A*Rez => B Î R

Теперь возьмем такие А и B и проверим найдется ли многочлен P'(x):

P(z) = (Az+B)(1-k)(2z+p)R(z)

P(z) - (Az+B)(1-k)(2z+p)R(z) = 0

z - корень многочлена P(x) - (Ax+B)(1-k)(2x+p)R(x), по теореме о комплексном корне z' также является корнем этого многочлена => P(x) - (Ax+B)(1-k)(2x+p)R(x) = (x-z)(x-z')P`(x) = (x²+px+q)P'(x)

Th Остроградского:

Пусть 1) P(x), Q(x) Î R[x] degP < degQ

2) Q(x) = (x-z₁)^k1...(x-z_s)^ks*(x²+xp₁+q₁)ⁿ¹...(x²+xp_m+q_m)^nm

x_i ¹ x_j (i ¹ j) x²+xp_i+q_i = (x-w_i)(x-w_i') w Ï R

3) Q₁(x) = (x-z₁)^k1-1...(x-z_s)^ks-1(x²+xp₁+q₁)^n1-1...(x²+xp_m+q_m)^nm-1

4) Q₂(x) = (x-z₁)...(x-z_s)(x²+xp₁+q₁)...(x²+xp_m+q_m), Q(x) = Q₁(x) * Q₂(x)

Тогда $ P₁(x), P₂(x) Î R[x]: P₁/Q₁, P₂/Q₂ - правильные дроби и òP(x)/Q(x)dx = P₁(x)/Q₁(x) + òP₂(x)/Q₂(x)dx

Доказательство: Q(x) = (x-z₁)^k1...(x-z_s)^ks(x²+xp₁+q₁)ⁿ¹...(x²+xp_m+q_m)^nm

k₁ + ... + k_s + n₁ + ... + n_m = r

1) r = 1: P(x)=P₂(x), P₁(x)=0, Q₂(x)=Q(x), Q₁(x)=1

2) r > 1: по индукции

Пусть для r = n-1 - верно

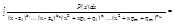
Интеграл, стоящий в сумме справа, раскладывается по индуктивному предположению => получаем:

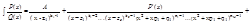
Справа в равенстве кроме интеграла имеем сумму двух правильных дробей обозначим их общий знаменатель Q₁, а числитель P₁, получим правильную дробь P₁/Q₁. Под интегралом обозначим знаменатель через Q₂, заметив, что под интегралом стоит правильная дробь и Q(x) = Q₁(x) * Q₂(x) получим, что для r = n теорема также верна.

6. Интегралы вида òR(x,(ax+b/cx+d)^m1, ...,(ax+b/cx+d)^mk)dx mi Î Q

òR(x,,...,)dx, mi Î Q, ad - bc ¹ 0

Определитель не равен нулю так как иначе коэффициенты a, b пропорциональны коэффициентам c, d и тогда отношение ax+b/cx+d от x не зависело бы. B этом случае подинтегральная функция была бы рациональной постоянной функцией и интегрировалась бы по таблице интегралов.

Пусть n - общий знаменатель чисел m₁,...,m_k, m_i = p_i/n, p_i Î Z, i = 1,...,k

=>

- рациональная ф-ция

dx = dR₀(t) = R₀`(t)dt, где R<sub>0</sub>`(t) - тоже рациональная ф-ция (ax+b/cx+d)^mi = t^pi=R_I(t), i = 1,...,k, отсюда получим:

òR(x,, ..., )dx = òR(R₀(t),R₁(t),...,R_K(t))R₀`(t)dt, т.о.вычисление исходного итеграла сводится к интегрированию рациональных дробей.