Среднее значение функции на отрезке.
Th: Пусть f, g Î L[a,b} и f(x) £ g(x) на [a,b], Тогда:
a) 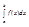 £
£ 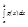 ,
,
б) Если дополнительно $ c Î [a,b]: d(c)-f(c) > 0 и g(x)-f(x) непрерывна в точке c, то 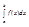 <
< 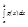
Доказательство:
a) h(x) = g(x) - f(x) ³ 0
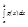 -
-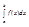 =
=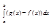 = S1...N(g(mI)-f(mI))D(xI) ³ 0 так как каждое слагаемое ³ 0 =>
= S1...N(g(mI)-f(mI))D(xI) ³ 0 так как каждое слагаемое ³ 0 => 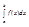 £
£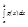
б) Если h(c) > 0, то: если x Î " E (c-d,c+d)&[a,b] => |h(x)-h(c)| < E
Возьмем E = h(c)/2 => h(c)/2 < h(x) < 3h(c)/2
$ I=[d-d/2,d+d/2]: x Î I => h(x) > h(c)/2
 - каждый интеграл в сумме ³ 0, т.к. если расписать их в суммы Римана все слагаемые будут больше 0 => если доказать, что хотя бы один из интегралов строго больше нуля => исходный интеграл строго больше нуля.
- каждый интеграл в сумме ³ 0, т.к. если расписать их в суммы Римана все слагаемые будут больше 0 => если доказать, что хотя бы один из интегралов строго больше нуля => исходный интеграл строго больше нуля.
По пункту a)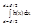 ³
³ , т.к.h(x)>h(c)/2, учитывая что
, т.к.h(x)>h(c)/2, учитывая что  = S1...N h(c)/2D(xI) = h(c)/2*S1...N D(xI) = h(c)/2 > 0, получим
= S1...N h(c)/2D(xI) = h(c)/2*S1...N D(xI) = h(c)/2 > 0, получим 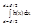 ³
³ >0 =>
>0 =>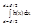 ³
³ >0=>
>0=>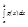 -
-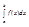 >0 =>
>0 =>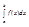 <
<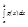 .
.
Th о среднем: Пусть f,g Î L[a,b], " x Î [a,b] d(x) ³ 0; m=inf f(x); M=supf(x), x Î [a,b], тогда $ l Î [m,M]: = l*
= l*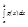
Доказательство: m £ f(x) £ M => mg(x) £ f(x)g(x) £ Mg(x) => m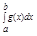 £
£ 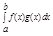 £ M
£ M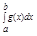
1)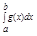 = 0 =>
= 0 =>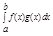 = 0 => берем l произвольно в частности можно и из [m,M]
= 0 => берем l произвольно в частности можно и из [m,M]
2) 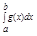 > 0 => m
> 0 => m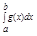 £
£ 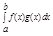 £ M
£ M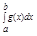 =>
=>
m £  £ M
£ M
Возьмем l = - оно сущ. и опр. однозначно. Для такого l теорема верна => $ l Î [m,M]:
- оно сущ. и опр. однозначно. Для такого l теорема верна => $ l Î [m,M]: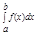 = l*
= l*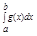
Замечание: Если в теореме о среднем f - непрерывна на [a,b], то $ x’, x’’: f(x’) = m & f(x’’) = M => $ c Î (x’;x''): f(c) = l
Доказательство: Если функция непрерывна на [a,b], то она достигает своего наибольшего и наименьшего значения на [a,b] => $ x’, x’’: f(x’) = m & f(x’’) = M. По теореме о среднем $ l Î [m,M] интеграл от f(x) равен l интегралам от g(x). По теореме о непрерывной функции $ c: l = f(c) причем c между x’ и x’’.
Частный случай теоремы о среднем:
g(x) = 1 =>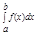 = l
= l = l(b-a) => l = 1/b-a *
= l(b-a) => l = 1/b-a * 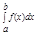 => l - среднее значение функции f на отрезке [a,b]
=> l - среднее значение функции f на отрезке [a,b]
Геометрический смысл среднего значения: $ такое l что площадь прямоугольника (l x b-a) равна площади криволинейной трапеции.