И дифференцируемость. Существование первообразной у непрерывной функции.
f Î L[a,b], F(x) = 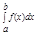 , x Î [a,b]
, x Î [a,b]
Th: Пусть f Î L[a,b], тогда F(x) =  - непрерывна на [a,b].
- непрерывна на [a,b].
Доказательство: Так как f Î L[a,b] => f - ограничена на [a,b] => $ M: |f(t)|<M
F(x + Dx) = = F(x) +
= F(x) +
|F(x+Dx) - F(x)| = | | £ |
| £ | | - переход к неравенству по свойству интеграла |
| - переход к неравенству по свойству интеграла | | £ |
| £ |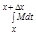 | = MDx (использовали то, что |f(t)|<M). => Получили |F(x+Dx) - F(x)| £ MDx => при Dx®0 F(x+Dx)®F(x) - определение непрерывности
| = MDx (использовали то, что |f(t)|<M). => Получили |F(x+Dx) - F(x)| £ MDx => при Dx®0 F(x+Dx)®F(x) - определение непрерывности
Th: Пусть f Î L[a,b] и f непрерывна в точке x Î [a,b], тогда d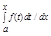 = f(x) или dF(x)/dx = f(x) или F’(x) = f(x)
= f(x) или dF(x)/dx = f(x) или F’(x) = f(x)
Доказательство: |(F(x+Dx)-F(x))/Dx - f(x)| = |1/Dx* - 1/Dx *
- 1/Dx * 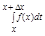 ) =1/Dx*
) =1/Dx* 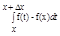 , где f(x) - константа
, где f(x) - константа
Из непрерывности f(t) в точке x получаем: " E>0 $ d>0: |t-x| < d => |f(t)-f(x)| < E
Возьмем Dx < d => |t-x| < Dx < d => |f(t)-f(x)| < E
Получили: 1/Dx* 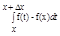 < 1/Dx*
< 1/Dx* =1/Dx*EDx = E => |(F(x+Dx)-F(x))/Dx - f(x)| < E
=1/Dx*EDx = E => |(F(x+Dx)-F(x))/Dx - f(x)| < E
Следствие: Если f(t) непрерывна на [a,b], то f имеет первообразную на [a,b]
Доказательство: Если f(t) непрерывна на [a,b] => она непрерывна на [a,x] (x Î[a,b]) => по теореме об интегрировании непрерывных функций существует  => существует функция F(x) =
=> существует функция F(x) =  , а по только что доказанной теореме F’(x)=f(x), т.е. F(x) является первообразной функции f.
, а по только что доказанной теореме F’(x)=f(x), т.е. F(x) является первообразной функции f.