Свойства скалярного произведения.
1. (a,b) = (b,a) {Следует из коммутативности произведения чисел и четности косинуса}
2. 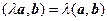 .
.
3. (а , b + c) = (a , b) + (a , c) .
{Два последних свойства следуют из соответствующих свойств проекций (§3) }
4. 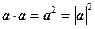 {Очевидно}
{Очевидно}
Скалярное произведение вектора на себя называют скалярным квадратом вектора. Последнее свойство утверждает, что скалярный квадрат вектора равен квадрату его длины.
Следующая теорема имеет принципиальное значение не только для векторного пространства, но и для любого его обобщения.
Теорема (необходимое и достаточное условие ортогональности). Два вектора взаимно ортогональны тогда и только тогда, когда их скалярное произведение равно нулю:
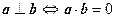
{Н.( 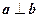 )
) 
Д.( 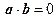 )
)  }
}
Указанные свойства позволяют легко вычислять скалярные произведения по известным характеристикам векторов.
Пример. Вычислить 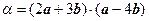 , если
, если 
{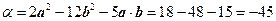 }
}
В действительности, более существенным является обратное утверждение: зная скалярные произведения, можно находить как длины векторов, так и углы между векторами:
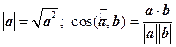
Однако, для того, чтобы пользоваться данными формулами, необходимо уметь вычислять скалярное произведение, зная только координаты векторов.
§7.Скалярное произведение в координатной форме.
Пусть векторы a и b заданы своими координатами в ортонормированном базисе { i, j, k }:
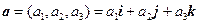 и
и  . Умножая скалярно a на b, получим
. Умножая скалярно a на b, получим

Для выбранного базиса выполняются соотношения:  Отсюда
Отсюда
получаем:  − Скалярное произведение в ортонормированном базисе
− Скалярное произведение в ортонормированном базисе
равно сумме попарных произведений координат.
Таким образом, имеем: 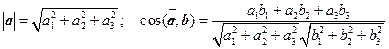
Пример. Вычислить длины векторов и косинус угла между ними: 
{ }
}
Замечание. В косоугольном базисе формула для выражения скалярного произведения через координаты будет, естественно, отличаться.
§8. Направляющие косинусы вектора.
Рассмотрим еще одну важную характеристику вектора.
Пусть задан ортонормированный базис { i, j, k } и произвольный вектор а .
Определение 1.Направляющими косинусами вектора а в данном базисе называются косинусы
углов между вектором а и базисными ортами:  .
.
Теорема 1. Направляющие косинусы единичного вектора равны его координатам.
{Пусть 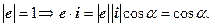 В координатах:
В координатах: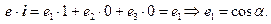 }
}
Теорема 2.Сумма квадратов направляющих косинусов равна единице: 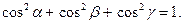
{Пусть а = (а1,а2,а3). Обозначим 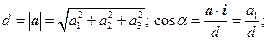 Аналогично
Аналогично

 }
}
Пример. Найти направляющие косинусывектораа = (4, −2, 4).
{
 }
}
§9.Ориентация базиса в пространстве.
Рассмотрим произвольную тройку некомпланарных векторов.
Определение. Упорядоченная тройка некомпланарных векторов называется правой , если
а) кратчайший поворот от первого вектора ко второму, видимый из конца третьего происходит против часовой стрелки (т.е. в положительном направлении), или б) по правилу винта, или
в) по правилу правой руки. В противном случае − левой. И в том и в другом случае тройка называется ориентированной.
Например, на рис.10 базис { i, j, k } − левый, а тройка {a, b, c} на рис.11 – правая.
 с Очевидно, что все одинаково ориентированные ортонормированные базисы могут
с Очевидно, что все одинаково ориентированные ортонормированные базисы могут
b быть совмещены друг с другом с помощью параллельного переноса и поворота,
a а противоположно ориентированные − только с точностью до коллинеарности.
Рис.11 Легко проверить, что тройки a b c, c a b и b c a одинаково ориентированы, а
тройки a c b, b a c и c b a им противоположны. Т.е. круговая перестановка векторов не
меняет ориентацию, а не круговая – меняет.
Изменение знака у одного из векторов меняет ориентацию всей тройки.
§10. Векторное произведение.
Определение.Векторным произведением векторов a и b : [a,b] называется вектор,
называется вектор,
удовлетворяющий трем условиям:
1. Векторное произведение ортогонально своим составляющим: 
2. Длина векторного произведения равна произведению длин векторов на синус угла между ними: 
3. Тройка векторов 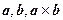 − правая.
− правая.