рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- СЛУЧАЙНЫЕ СОБЫТИЯ. ОСНОВНЫЕ ПОНЯТИЯ
Реферат Курсовая Конспект
СЛУЧАЙНЫЕ СОБЫТИЯ. ОСНОВНЫЕ ПОНЯТИЯ
СЛУЧАЙНЫЕ СОБЫТИЯ. ОСНОВНЫЕ ПОНЯТИЯ - раздел Математика, Теория вероятности Случайным Называется Событие, Которое При Осуществлении Совок...
Случайным называется событие, которое при осуществлении совокупности некоторых условий S может либо произойти, либо не произойти. Пример: событие А1 - выпадение “шестерки” при одном броске игральной кости (кубика с занумерованными гранями).
Достоверным называют событие, которое обязательно произойдет, если будет осуществлена совокупность условий S. Пример: событие А2 - при одном броске игральной кости число выпавших очков меньше 7. Обозначим достоверное событие буквой W.
Невозможным называют событие, которое заведомо не произойдет при осуществлении совокупности событий S. Пример: событие А3 - при одном броске игральной кости число выпавших очков дробно. Невозможное событие обозначим символом Æ.
События W и Æ будем рассматривать как частные (“крайние”) случаи случайных событий, хотя они не являются таковыми.
Два или более событий назовем несовместными, если в результате осуществления условий S (или, по-другому, в результате испытания) невозможно их совместное осуществление, т.е. появление одного из них исключает появление другого в том же испытании. Пример: событие А4 - при броске игральной кости выпало нечетное число очков - несовместно с событием А1 (выпала “шестерка”).
§2. СЛУЧАЙНЫЕ СОБЫТИЯ. ОПЕРАЦИИ
Сумма событий А + В - событие, состоящее в том, что произошло хотя бы одно из двух событий А и В, т.е. наступило либо А, либо В, либо оба сразу. Пример: для событий А1 и А4 из §1 А1 + А4 = {выпало 1,3,5 или 6 очков}.
Произведение событий А · В - это совместное осуществление и А и В (иначе: их общие исходы). Пусть В = {при броске игральной кости выпало число очков, кратное 3}. Тогда В · А4 = {выпала грань с 3 очками}.
Для несовместных событий А и В их произведение А·В=Æ : у них нет общих исходов. В частности, для последнего примера §1 можно записать А1 ·А4 = Æ.
Событие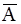 
называется противоположным к А (т.е. состоит в том, что “ достоверное событие W происходит, а событие А не происходит”).
Для операций над событиями выполняются свойства:
| А + В = В + А |
| А · В = В · А |
| (А + В) + С = А + (В + С) |
| (А · В) · С = А · (В · С) |
| (А + В) · С = А · С + В · С |
Если события Н1, Н2, ..., Нn попарно несовместны (Нi·Hj=Æ при i ¹ j ), а их сумма - достоверное событие (H1+H2+...+Hn = W ), то говорят, что {H1, H2, ..., Hn} - полная группа несовместных событий или разбиение W. В частности, {A,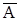
} - полная группа несовместных событий для любого А.
§3. КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ
Вероятность события А - это число Р(А), которое вводится для количественного описания степени объективной возможности наступления А.
В этом параграфе рассмотрим испытания, в которых множество W представляет собой конечное число равновозможных исходов. Например, если бросить игральную кость один раз, то она может выпасть на любую из шести граней. Достоверное событие W здесь состоит в том, что выпала одна из шести граней. Будем считать кубик симметричным; в этом случае можно считать все шесть исходов равновозможными. В случае двух бросков симметричной монеты - 4 различных исхода: “орел-орел” (О, О), “орел-решка”(О, Р), а также Р, О и Р, Р; их также считают равновозможными. Все они вместе образуют достоверное событие W для данного испытания. В первом случае вероятность каждого из элементарных исходов равна 1/6, а во втором 1/4.
В общем случае, если число всех элементарных исходов N(W) равно n, то вероятность каждого из них 1/n. Пусть число благоприятствующих исходов для А или, иначе, число элементарных исходов испытания, входящих в событие А ( N(A) ), равно m, тогда вероятность
( 1 )
Это формула классической вероятности.
В примерах из §1 шесть элементарных исходов: выпала цифра 1, 2, 3, 4, 5 или 6. Событие А1 включает в себя ровно 1 элементарный исход, А2 (достоверное) - все 6, А3 (невозможное) - 0, А4 - 3. Поэтому
, 
,
, 
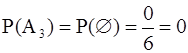Еще примеры. При двух бросках симметричной монеты событие С = {выпал хотя бы один “орел”} включает в себя три элементарных исхода из четырех, поэтому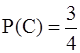 
.
Событию D = {при трех бросках монеты выпало ровно два ”орла”} благоприятствуют 3 из 8 возможных элементарных исходов, поэтому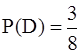 
.
– Конец работы –
Эта тема принадлежит разделу:
Теория вероятности
Государственное образовательное учреждение... высшего профессионального образования...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: СЛУЧАЙНЫЕ СОБЫТИЯ. ОСНОВНЫЕ ПОНЯТИЯ
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?
Подпишитесь на Нашу рассылку
Реклама
Информация в виде рефератов, конспектов, лекций, курсовых и дипломных работ имеют своего автора, которому принадлежат права. Поэтому, прежде чем использовать какую либо информацию с этого сайта, убедитесь, что этим Вы не нарушаете чье либо право.
© copyright 1999 - 2024 allRefs.net. Все права защищены. Страница сгенерирована за: 0.035 сек.
Новости и инфо для студентов