Производные и дифференциалы высших порядков.
Если функция 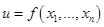 , определенная в некоторой области
, определенная в некоторой области  , имеет частную производную
, имеет частную производную 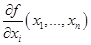 по переменной
по переменной 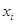 , то эта частная производная вновь является некоторой функцией, которая в свою очередь может иметь частную производную
, то эта частная производная вновь является некоторой функцией, которая в свою очередь может иметь частную производную 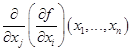 . Эта функция называется второй производной функции
. Эта функция называется второй производной функции 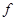 по переменным
по переменным 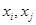 и обозначается символом
и обозначается символом 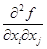 . Порядок индексов указывает, в каком порядке производится дифференцирование по соответствующим переменным.
. Порядок индексов указывает, в каком порядке производится дифференцирование по соответствующим переменным.
Мы определили частные производные второго порядка.
Если определена частная производная
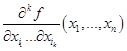
порядка 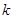 , то по индукции определяем частную производную порядка
, то по индукции определяем частную производную порядка 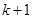 соотношением
соотношением
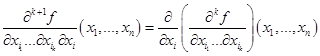 .
.
Когда функции записываются в виде  , вторые или третьи частные производные часто обозначаются следующим образом:
, вторые или третьи частные производные часто обозначаются следующим образом: 
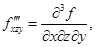
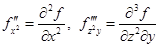 и так далее.
и так далее.
Возникает вопрос о том, влияет ли порядок дифференцирования на вычисленную частную производную. В общем случае влияет, но если функция удовлетворяет некоторым условиям, то нет. Сформулируем соответствующую теорему для случая функции двух переменных.
Теорема (Шварца). Если функция  непрерывна вместе со своими вторыми частными производными в некоторой окрестности
непрерывна вместе со своими вторыми частными производными в некоторой окрестности 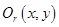 , точки
, точки 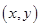 , то
, то
 .
.
Доказательство.  Введем вспомогательную функцию
Введем вспомогательную функцию
 ,
,
где смещение  предполагается достаточно малым, чтобы
предполагается достаточно малым, чтобы 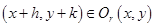 .
.
Функцию 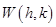 можно представить как разность
можно представить как разность
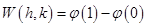 ,
,
где 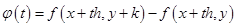 . Тогда по формуле конечных приращений имеем
. Тогда по формуле конечных приращений имеем
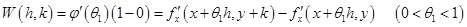 .
.
Применяя формулу конечных приращений к последней разности, получим
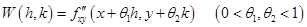 . (1)
. (1)
Если теперь представить 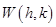 в виде разности
в виде разности
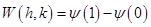 ,
,
где 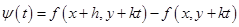 , то аналогичным образом найдем, что
, то аналогичным образом найдем, что
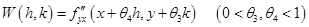 . (2)
. (2)
Сравнивая равенства (1) и (2), заключаем, что
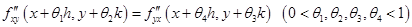 .
.
Воспользовавшись непрерывностью рассматриваемых частных производных в точке 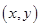 при
при 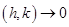 , получаем нужное нам равенство.
, получаем нужное нам равенство.
Следствие. Пусть функция 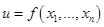 определена и непрерывна вместе со всеми своими частными производными до
определена и непрерывна вместе со всеми своими частными производными до  го порядка включительно.
го порядка включительно.
Тогда значение любой  й смешанной производной не зависит от того порядка, в котором производятся последовательные дифференцирования.
й смешанной производной не зависит от того порядка, в котором производятся последовательные дифференцирования.