Дифференциалы высших порядков.
Пусть в области  задана некоторая функция
задана некоторая функция 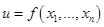 , имеющая непрерывные частные производные первого порядка. Тогда она будет дифференцируема в этой области, и ее дифференциал имеет вид
, имеющая непрерывные частные производные первого порядка. Тогда она будет дифференцируема в этой области, и ее дифференциал имеет вид
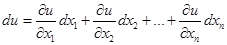 ,
,
где 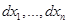 - произвольные приращения независимых переменных
- произвольные приращения независимых переменных 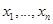 .
.
Видим, что 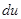 также является функцией от
также является функцией от 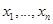 . Если существуют непрерывные частные производные второго порядка функции для
. Если существуют непрерывные частные производные второго порядка функции для  , то можно говорить о дифференциале от первого дифференциала
, то можно говорить о дифференциале от первого дифференциала  , который называется дифференциалом второго порядка от
, который называется дифференциалом второго порядка от  и обозначается символом
и обозначается символом 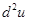 .
.
Приращения 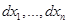 при этом рассматриваются как постоянные и остаются одними и теми же при переходе от одного дифференциала к следующему.
при этом рассматриваются как постоянные и остаются одними и теми же при переходе от одного дифференциала к следующему.
Запишем формулу второго дифференциала для функции двух переменных 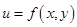 :
:
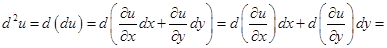

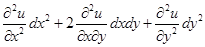 .
.
Если первый дифференциал символически записать следующим образом
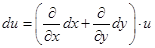 ,
,
то второй будет иметь вид
 .
.
Можно показать, что аналогичная формула справедлива для дифференциалов любого порядка от функций любого же количества переменных 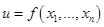 :
:
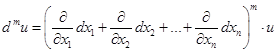 .
.