Необходимые условия относительного экстремума.
Рассмотрим случай поиска условного экстремума функции двух переменных при наличии одного уравнения связи.
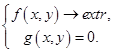 (1)
(1)
Теорема. Пусть функции 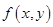 и
и  имеют непрерывные смешанные производные в окрестности точки
имеют непрерывные смешанные производные в окрестности точки  , причем
, причем 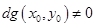 , и пусть
, и пусть  - точка условного экстремума в задаче (1).
- точка условного экстремума в задаче (1).
Тогда существует число 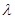 (множитель Лагранжа) такое, что
(множитель Лагранжа) такое, что 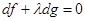 .
.
Доказательство. 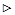 Из условия
Из условия 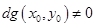 следует, что
следует, что  и
и  не могут быть равны нулю одновременно. Пусть, например,
не могут быть равны нулю одновременно. Пусть, например, 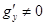 . Тогда по теореме о неявной функции в некоторой окрестности
. Тогда по теореме о неявной функции в некоторой окрестности  переменную
переменную 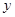 можно явно выразить через переменную
можно явно выразить через переменную  , причем функция
, причем функция 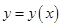 будет непрерывной и дифференцируемой в этой окрестности, а ее производная вычисляется по формуле
будет непрерывной и дифференцируемой в этой окрестности, а ее производная вычисляется по формуле 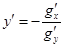 .
.
Точка 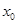 в таком случае будет точкой абсолютного экстремума сложной функции
в таком случае будет точкой абсолютного экстремума сложной функции  . Необходимым условием экстремума дифференцируемой функции одной переменной является равенство нулю производной. Запишем это условие:
. Необходимым условием экстремума дифференцируемой функции одной переменной является равенство нулю производной. Запишем это условие:
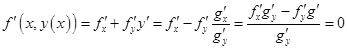 .
.
То есть 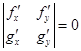 . Равенство нулю определителя означает линейную зависимость его строк. То есть равенство нулю некоторой нетривиальной линейной комбинации строк:
. Равенство нулю определителя означает линейную зависимость его строк. То есть равенство нулю некоторой нетривиальной линейной комбинации строк:
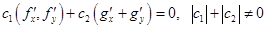 .
.
Так как 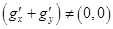 , то
, то  и можно положить
и можно положить 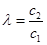 . И мы получаем равенство
. И мы получаем равенство
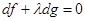 .
.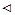
Итак, в точке условного экстремума необходимо должно выполняться
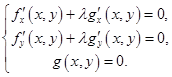
Если ввести вспомогательную функцию (функцию Лагранжа)  , то уравнения последней системы означают равенство нулю ее дифференциала, то есть решение этой системы
, то уравнения последней системы означают равенство нулю ее дифференциала, то есть решение этой системы  является точкой стационарности функции
является точкой стационарности функции 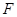 .
.
В общем случае надо искать точки стационарности функции
 .
.