Достаточные условия относительного экстремума.
Вернемся к задаче (1)
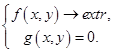
Пусть функции 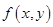 и
и  имеют непрерывные вторые смешанные производные в окрестности точки
имеют непрерывные вторые смешанные производные в окрестности точки  , причем
, причем 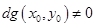 , и пусть
, и пусть  - точка стационарности функции Лагранжа
- точка стационарности функции Лагранжа  .
.
Отметим, что если переменные  удовлетворяют уравнению связи
удовлетворяют уравнению связи 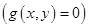 , то справедливо равенство
, то справедливо равенство  , поэтому при этих условиях точка
, поэтому при этих условиях точка  будет точкой экстремума функций
будет точкой экстремума функций 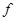 и
и 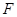 одновременно.
одновременно.
Займемся вопросом существования экстремума функции 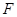 в точке
в точке  . Запишем приращение
. Запишем приращение 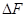 по формуле Тейлора, учитывая, что
по формуле Тейлора, учитывая, что  :
:
 .
.
Можно показать, что при условии строгой положительности или отрицательности второго дифференциала, знак разности для достаточно малых приращений переменных определяется знаком первого слагаемого.
Распишем второй дифференциал:

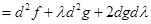 .
.
Так как при наших условиях 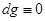 , то получаем, что знак приращения
, то получаем, что знак приращения  совпадает со знаком выражения
совпадает со знаком выражения
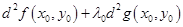 .
.
Таким образом, в нашей точке  будет относительный минимум, если
будет относительный минимум, если
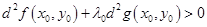
и максимум, если
 .
.
Или

В общем случае
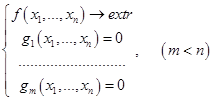 ,
,
достаточным условием существования относительного экстремума является сохранение в окрестности критической точки знака второго дифференциала функции Лагранжа
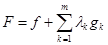
при условии, что переменные 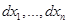 связаны соотношением
связаны соотношением
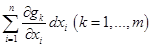 .
.