Первообразные рациональных функций
Первообразные рациональных функций
Рассмотрим интегралы вида 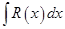 , где
, где 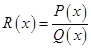 - отношение полиномов. Из алгебры известно, что любую такую дробь можно представить в виде
- отношение полиномов. Из алгебры известно, что любую такую дробь можно представить в виде
 ,
,
(дискриминанты знаменателей дробей второй суммы отрицательны).
Дроби вида 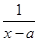 ,
, 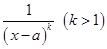 ,
, 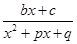 и
и  называются простейшими рациональными дробями соответственно
называются простейшими рациональными дробями соответственно 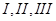 и
и 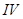 рода.
рода.
Имеем
 ,
,

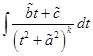 ,
,
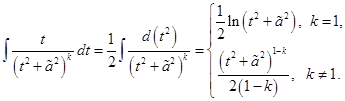
Рассмотрим интегралы  . Интегрируя по частям, имеем
. Интегрируя по частям, имеем

 ,
,
то есть
 .
.
Пример1. 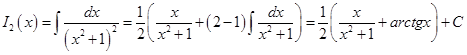 .
.
Пример 2.
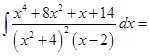
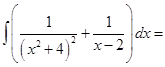
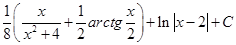 .
.
 ,
,
умножим левую и правую части равенства на знаменатель левой части:
 ,
,
поскольку наши многочлены равны, то равны их значения в точке  :
:
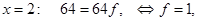
равны коэффициенты при 
 .
.
А для определения оставшихся трех коэффициентов, приравняем значения еще в трех точках:
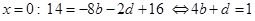 ,
,
 ,
,
 ,
,
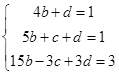 ,
,
 .
.
Пример 3.  .
.



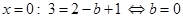 .
.
Первообразные вида .
, получаем .Первообразные вида .
В этом случае подынтегральное выражение рационализируется при помощи подстановки 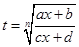 .
.
Пример 7. 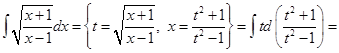

 , где
, где 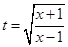 .
.
Первообразные вида .
В этом случае подынтегральное выражение рационализируется при помощи подстановки  .
.
Пример 8. 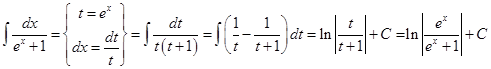 .
.
Первообразные вида . Подстановки Эйлера.
Выделяя полный квадрат в трехчлене 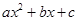 и делая соответствующую линейную замену переменной, интеграл можно привести к одному из следующих видов:
и делая соответствующую линейную замену переменной, интеграл можно привести к одному из следующих видов:
, , .
Для рационализации этих интегралов достаточно положить, соответственно:
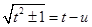 (тогда
(тогда  ;
;  ;
;  ;
;  );
);
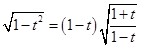 ;
;  (тогда
(тогда  ;
;  ).
).
Эти подстановки были предложены еще Эйлером.
Можно воспользоваться тригонометрическими или гиперболическими подстановками.
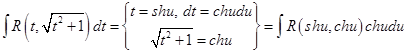 .
.
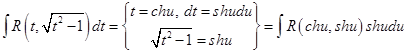 .
.
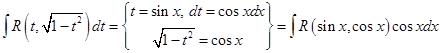 .
.
Пример 9. 
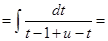
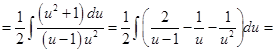
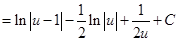 , где
, где 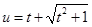 и
и 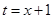 .
.
Пример 10. 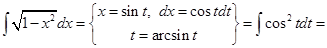
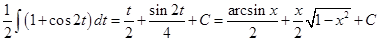 .
.