Утверждение.
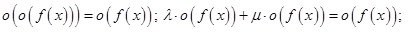

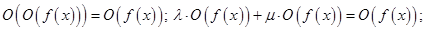
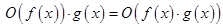 .
.
Теорема. Пусть непрерывные в нуле функции 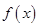 и
и 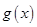 эквивалентны при
эквивалентны при  , а функция
, а функция  бесконечно малая при
бесконечно малая при 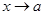 .
.
Тогда функция  будет эквивалентна функции
будет эквивалентна функции 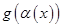 при
при 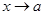 .
.
Аналогично предыдущей доказывается теорема:
Теорема. Пусть 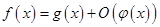 , где
, где  при
при  . И пусть
. И пусть  - бесконечно малая при
- бесконечно малая при 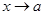 , причем
, причем 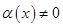 в
в 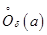 .
.
Тогда 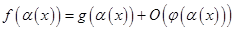 при
при 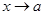 .
.
Приведем асимптотические представления для основных элементарных функций при  :
:
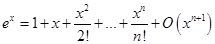 ,
,
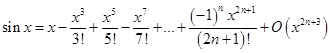 ,
, ,
, ,
,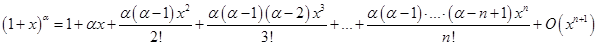 .
.
Разберем несколько примеров.
Пример 1. Написать асимптотическую формулу для  при
при  (записать два члена асимптотики, не считая остатка).
(записать два члена асимптотики, не считая остатка).
Решение.  , где
, где  - бесконечно малая при
- бесконечно малая при  ,
,

 .
.
Пример 2. Написать асимптотическую формулу для  при
при  (записать два члена асимптотики, не считая остатка).
(записать два члена асимптотики, не считая остатка).
Решение. 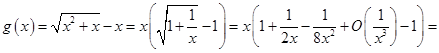
 , где
, где  - бесконечно малая при
- бесконечно малая при  ;
;
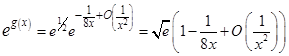 .
.
Пример 3. Написать асимптотическую формулу для  при
при  (записать два члена асимптотики, не считая остатка).
(записать два члена асимптотики, не считая остатка).
Решение. 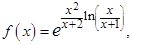
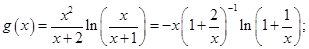
 ;
;
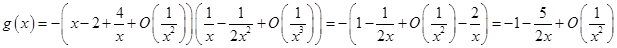
(все остальные слагаемые в последнем произведении «поглощены» 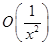 ). Таким образом
). Таким образом
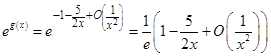 .
.