Асимптотические формулы для функций, заданных в виде интегралов.
Пусть функция 
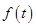 непрерывна на полуоси
непрерывна на полуоси  . Нас будет интересовать поведение функции
. Нас будет интересовать поведение функции 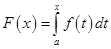 при
при  .
.
Теорема. Пусть положительные функции 
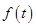 ,
, 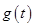 непрерывны на полуоси
непрерывны на полуоси  . Обозначим
. Обозначим 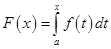 ,
, 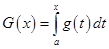 .
.
Тогда если  и
и 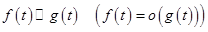 при
при  , то
, то  при
при  .
.
Доказательство. 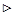 Пусть
Пусть  . Согласно условию теоремы, интеграл
. Согласно условию теоремы, интеграл 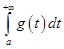 расходится, поэтому по теореме сравнения для несобственных интегралов расходится также и интеграл
расходится, поэтому по теореме сравнения для несобственных интегралов расходится также и интеграл  , то есть
, то есть 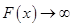 . Следовательно, при нахождении предела отношения функций
. Следовательно, при нахождении предела отношения функций  и
и 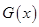 мы можем воспользоваться правилом Бернулли-Лопиталя. Итак, получаем
мы можем воспользоваться правилом Бернулли-Лопиталя. Итак, получаем
 .
.
Пусть теперь 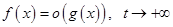 . Если интеграл
. Если интеграл  сходится, то существует конечный предел
сходится, то существует конечный предел 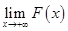 и
и  . Если же
. Если же 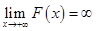 , то воспользуемся правилом Бернулли-Лопиталя:
, то воспользуемся правилом Бернулли-Лопиталя:
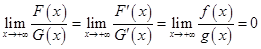 .
.
Во всех случаях 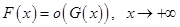 .
.
Пример 5. Написать асимптотическое представление функции, заданной интегралом: (записать два члена асимптотики).
(записать два члена асимптотики).
Здесь 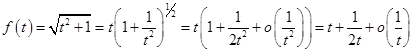 ,
,
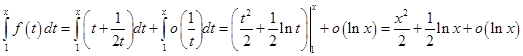 .
.
Пример 6. Написать асимптотическое представление функции, заданной интегралом: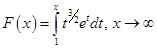 (записать два члена асимптотики).
(записать два члена асимптотики).
Воспользуемся формулой интегрирования по частям:
 ,
,
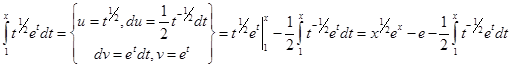 .
.
Так как 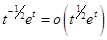 , то
, то 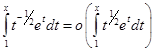 и
и 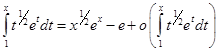 . Это означает, что
. Это означает, что 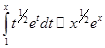 и
и 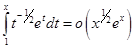 . Окончательно получаем
. Окончательно получаем
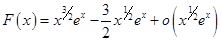 .
.
Докажем еще одну теорему:
Теорема. Пусть положительные функции 
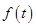 ,
, 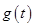 непрерывны на полуоси
непрерывны на полуоси  . Обозначим
. Обозначим 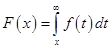 ,
, 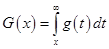 .
.
Тогда если 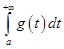 сходится и
сходится и 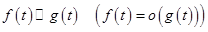 при
при  , то
, то  при
при  .
.
Доказательство. 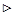 Пусть
Пусть  . Согласно условию теоремы, интеграл
. Согласно условию теоремы, интеграл 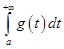 сходится, поэтому по теореме сравнения для несобственных интегралов сходится также и интеграл
сходится, поэтому по теореме сравнения для несобственных интегралов сходится также и интеграл  , то есть
, то есть 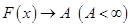 , то есть
, то есть 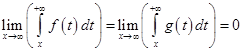 . Следовательно, при нахождении предела отношения функций
. Следовательно, при нахождении предела отношения функций  и
и 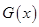 мы можем воспользоваться правилом Бернулли-Лопиталя. Итак, получаем
мы можем воспользоваться правилом Бернулли-Лопиталя. Итак, получаем
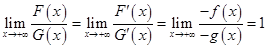 .
.
Пусть теперь 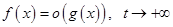 . Очевидно, что интеграл
. Очевидно, что интеграл  сходится, то есть
сходится, то есть 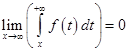 , поэтому мы можем воспользоваться правилом Бернулли-Лопиталя:
, поэтому мы можем воспользоваться правилом Бернулли-Лопиталя:
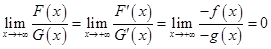 .
.
Пример 7. Написать асимптотическое представление функции, заданной интегралом: (записать два члена асимптотики).
(записать два члена асимптотики).
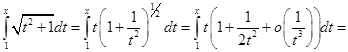
 .
.
Поскольку константа 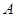 нам неизвестна, мы можем только записать
нам неизвестна, мы можем только записать

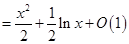 .
.