рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- МАТРИЦЫ ОПЕРАТОРОВ МОМЕНТА ИМПУЛЬСА
Реферат Курсовая Конспект
МАТРИЦЫ ОПЕРАТОРОВ МОМЕНТА ИМПУЛЬСА
МАТРИЦЫ ОПЕРАТОРОВ МОМЕНТА ИМПУЛЬСА - раздел Математика, Л Е К Ц И Я 11 ...
Л Е К Ц И Я 11
МАТРИЦЫ ОПЕРАТОРОВ МОМЕНТА ИМПУЛЬСА
Мы хотим найти матрицы спиновых операторов 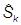 в явном виде. Для этого решим сначала более общую задачу - найдем матрицы операторов момента
в явном виде. Для этого решим сначала более общую задачу - найдем матрицы операторов момента  и
и 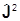 , которые удовлетворяют коммутационным соотношениям
, которые удовлетворяют коммутационным соотношениям
[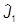 ,
, ]=i
]=i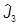 , [
, [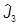 ,
,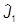 ]=i
]=i , [
, [ ,
,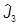 ]=i
]=i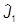 , [
, [ ,
,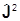 ]=
]=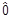 , (пока
, (пока  =1!).
=1!).
Пользоваться будем только этими коммутационными соотношениями. Так как 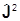 и
и 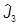 коммутируют, то можно искать их общие собственные векторы:
коммутируют, то можно искать их общие собственные векторы:
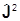 |
|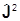 ,mñ = J2|
,mñ = J2|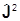 ,mñ,
,mñ, 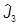 |
|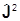 ,mñ = m|
,mñ = m|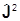 ,mñ.
,mñ.
Пусть J2 фиксировано. Это означает, что мы рассматриваем подпространство всех векторов состояний, в которых J2 имеет определенное значение, а m изменяется. Векторы |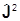 ,mñ образуют в таком подпространстве базис. Ближайшая цель - найти матрицы операторов
,mñ образуют в таком подпространстве базис. Ближайшая цель - найти матрицы операторов  в этом базисе, который называется каноническим, и который для краткости обозначим как |mñ.
в этом базисе, который называется каноническим, и который для краткости обозначим как |mñ.
Для ее решения удобно ввести операторы
 + =
+ =  1 + i
1 + i 2,
2,  _ =
_ =  ++ =
++ =  1 - i
1 - i 2,
2,
которые, как легко показать прямой проверкой, удовлетворяют коммутационным соотношениям
[ +,
+, _] = 2
_] = 2 3, [
3, [ _,
_, 3] =
3] =  _, [
_, [ 3,
3, +] =
+] =  +.
+.
Покажем, что
 +|mñ = am|m+1ñ,
+|mñ = am|m+1ñ,  _|mñ = bm|m-1ñ,
_|mñ = bm|m-1ñ,
где am и bm - некоторые числа, которые без ограничения общности можно считать вещественными. Имеем, используя коммутационное соотношение,
 3(
3( _|mñ) = (
_|mñ) = ( _
_ 0-
0- _)|mñ = (
_)|mñ = ( -m-
-m- _)|mñ = (m-1)(
_)|mñ = (m-1)( _|mñ),
_|mñ),
и аналогично
 3(
3( +|mñ) = (m +1)(
+|mñ) = (m +1)( +|mñ).
+|mñ).
Таким образом,  _|mñ и
_|mñ и  +|mñ - собственные векторы оператора с собственными значениями m-1 и m+1 соответственно, что фактически и утверждалось.
+|mñ - собственные векторы оператора с собственными значениями m-1 и m+1 соответственно, что фактически и утверждалось.
Теперь задача отыскания матриц операторов  свелась фактически к нахождению чисел am и bm и спектра оператора
свелась фактически к нахождению чисел am и bm и спектра оператора  3. Учитывая, что базисные векторы предполагаются нормированными, имеем:
3. Учитывая, что базисные векторы предполагаются нормированными, имеем:
ám| ++|m+1ñ = amám+1|m+1ñ = am = ám|
++|m+1ñ = amám+1|m+1ñ = am = ám| _|m+1ñ = bm+1
_|m+1ñ = bm+1 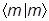 = bm+1,
= bm+1,
откуда вытекает соотношение между bm и am:
bm+1 = am.
Чтобы получить числа am , проделаем следующую выкладку:
 +|m-1ñ = am-1|mñ =
+|m-1ñ = am-1|mñ = 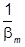
 +
+ _|mñ =
_|mñ = 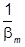 (
( _
_ ++2
++2 3) |mñ =
3) |mñ =
= 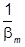 (bm+1am + 2m)|mñ,
(bm+1am + 2m)|mñ,
или, с учетом предыдущего равенства,
a2m-1 - a2m = 2m.
Получили рекуррентное соотношение для am. Введем обозначение
j = max m,
и сложим все предыдущие равенства от m = j до произвольного m + 1:
a2m - a2j = 2j + 2(j - 1) +...+ 2(m +1) = j(j +1) - m(m +1).
Учтем теперь, что aj = 0, так j - это максимальное m,
 +| j ñ = aj| j + 1ñ,
+| j ñ = aj| j + 1ñ,
и если бы aj ¹ 0, то мы получили бы еще большее m, равное j+1. Поэтому
a2m = j(j +1) - m(m +1)
и
b2m = a2m-1 = j(j +1) - m(m - 1).
Таким образом, операторы  +,
+,  _ и
_ и  3 действуют на базисные векторы |mñ по закону
3 действуют на базисные векторы |mñ по закону
 +|mñ =
+|mñ = 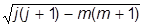 |m+1ñ,
|m+1ñ,
 _|mñ =
_|mñ = 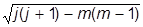 |m-1ñ,
|m-1ñ,
 3|mñ = m|mñ.
3|mñ = m|mñ.
Действуя последовательными степенями  _ на |jñ, получим набор собственных векторов
_ на |jñ, получим набор собственных векторов
|jñ, |j-1ñ, |j-2ñ,....
Последним в нем будет вектор |-jñ, так как из второй полученной формулы следует  _|-jñ=0. Таким образом, наименьшим собственным значением оператора
_|-jñ=0. Таким образом, наименьшим собственным значением оператора  3 является число -j:
3 является число -j:
min {m} = -j.
Так как при таком построении число m на каждом этапе уменьшается на 1, то разность j-(-j)=2j должна быть целым числом, откуда j - целое или полуцелое число. Размерность подпространства с фиксированным значением j равна 2j+1 ( именно столько векторов |mñ оно содержит), т.е. она определяется максимальным собственным значением оператора  3.
3.
Докажем теперь, что каждый из векторов |mñ действительно является собственным для оператора 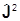 ( ведь мы его так обозначили лишь для краткости, а на самом деле это |
( ведь мы его так обозначили лишь для краткости, а на самом деле это |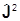 ,mñ), и найдем соответствующее собственное значение ( оно должно быть единым, ибо
,mñ), и найдем соответствующее собственное значение ( оно должно быть единым, ибо 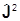 - фиксировано). Для этого перепишем
- фиксировано). Для этого перепишем 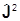 в виде
в виде
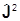 =
=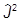 1 +
1 +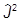 2 +
2 +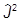 3 =
3 = +
+ _ -
_ -  3 +
3 + 3.
3.
Действуем этим оператором на произвольный базисный орт:
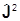 |mñ = (
|mñ = (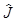 +
+ 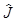 --
--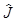 3+
3+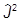 3)|mñ = (am-1bm-m+m2) |mñ = (b2m -m+m2) |mñ.
3)|mñ = (am-1bm-m+m2) |mñ = (b2m -m+m2) |mñ.
Подставляя сюда найденное ранее b2m, получим
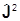 |mñ = j(j +1)|mñ.
|mñ = j(j +1)|mñ.
Таким образом, все |mñ действительно собственные векторы для 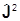 , причем они обладают одним и тем же собственным значением, как это и должно быть. Это собственное значение равно j(j +1).
, причем они обладают одним и тем же собственным значением, как это и должно быть. Это собственное значение равно j(j +1).
Подведем предварительные итоги. По отношению к действию оператора квадрата момента 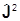 все пространство разбивается на подпространства, в которых он кратен единичному оператору:
все пространство разбивается на подпространства, в которых он кратен единичному оператору:
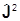 = j(j +1)
= j(j +1)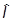 .
.
Размерность каждого подпространства равна 2j+1, где j - произвольное (но фиксированное для подпространства) целое или полуцелое число. Канонический базис в каждом подпространстве образует собственные векторы оператора  3, собственные значения которого меняются через 1 в пределах
3, собственные значения которого меняются через 1 в пределах
-j £ m £ j.
Эти собственные векторы будем обозначать как |jmñ, куда входит и индекс подпространства j и индекс базисного орта m. Для них
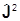 |jmñ = j(j +1) |jmñ,
|jmñ = j(j +1) |jmñ,  3|jmñ = m|jmñ.
3|jmñ = m|jmñ.
Произвольный вектор |yñ гильбертова пространства состояний можно разложить по всем таким базисным ортам:
|yñ =  Cjm|jmñ.
Cjm|jmñ.
Найдем теперь матрицы операторов момента в построенном базисе. Умножая формулы
 +|mñ =
+|mñ =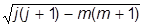 |m+1ñ,
|m+1ñ,
 _|mñ =
_|mñ =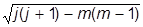 |m-1ñ,
|m-1ñ,
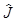 3|mñ =m|mñ.
3|mñ =m|mñ.
слева на án| и, учитывая ортонормированность базиса,
án| mñ = dnm,
получим
án| +(j)|mñ º ( J+(j))nm =
+(j)|mñ º ( J+(j))nm = 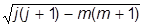 dn,m+1
dn,m+1
án| _(j) | mñ º (J_(j))nm =
_(j) | mñ º (J_(j))nm = 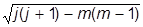 dn,m-1
dn,m-1
án| 3(j) | mñ º (J3(j))nm = mdn,m.
3(j) | mñ º (J3(j))nm = mdn,m.
Имея в виду, что
 1 =
1 =  (
( _+
_+ +),
+),  2 =
2 = 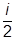 (
( _+
_+ +)
+)
и восстанавливая теперь  , которое мы раньше для простоты записи положили равным 1, придем к следующему окончательному результату:
, которое мы раньше для простоты записи положили равным 1, придем к следующему окончательному результату:
( J1(j))nm =
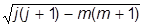 dn,m+1 +
dn,m+1 +
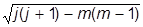 dn,m-1
dn,m-1
(J2(j))nm = -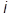
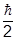
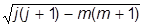 dn,m+1 +
dn,m+1 +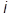
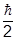
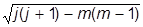 dn,m-1
dn,m-1
( J3(j))nm =  m dn,m
m dn,m
( J2(j))nm =  2j(j+1) dn,m.
2j(j+1) dn,m.
Здесь перечислены все возможные матрицы операторов момента, которые будут получаться, когда j пробегает значения 0, 1/2, 1, 3/2,.... Когда мы рассматривали орбитальный момент, то для него получили только целые значения j , которые обозначились как l. Но оказывается, что полуцелые значения также имеют глубокий смысл - они соответствуют спиновому моменту (разумеется, у некоторых частиц спин может быть и целым, но его природа совсем другая, чем природа орбитального момента).
Ввиду важности для дальнейшего, выпишем матрицы операторов момента для случая j = 1/2, когда m принимает значения m = +1/2 и m= -1/2. Делается это так:
(J1)11 º (J1)+1/2, +1/2 = 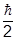
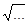 d1/2,3/2 +
d1/2,3/2 + 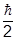
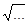 d1/2,-1/2 = 0.
d1/2,-1/2 = 0.
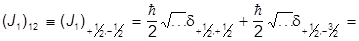
= 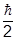
 .
.
В итоге получим
J1 =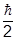
 , J2 =
, J2 = 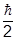
 , J3 =
, J3 = 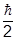
 , J2 =3/4
, J2 =3/4  2
2  .
.
Если ввести матрицы Паули
s1 =  , s2 =
, s2 =  , s3 =
, s3 =  ,
,
то можно будет записать
Jk = 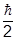 sk, J2 =
sk, J2 =  s2.
s2.
СПИН
До сих пор мы считали, что всякая квантовая частица имеет три степени свободы. Это подразумевало, что полный набор включает три наблюдаемых - например, x,y,z. Это, в свою очередь, и позволяло описывать состояния частицы в координатном представлении одной волновой функцией
y = y(x,y,z) º y(r).
Но постепенно выяснилось, что у микрочастиц число степеней свободы больше трех. Об этом свидетельствовали: (а) опыты Штерна-Герлаха, (б) дублетная структура спектров у щелочных металлов - например, наличие в спектре натрия яркого желтого дублета, (в) аномальный эффект Зеемана - расщепление не на три линии, а на большее количество. После долгих мучений В. Паули ввел представление о «характерной двузначности» электрона, т.е. об удвоении числа его состояний. Но было неясно, что же это такое на самом деле. В 1925 г. Гаудсмит и Улэнбек предположили, что у электрона есть собственный (а не только) орбитальный момент импульса - спин, равный 1/2. Вскоре Паули построил соответствующий математический аппарат. Не нужно думать, что спин связан с каким-то вращением электрона - эта модель сразу приводит к противоречиям: например, скорость на «экваторе» электрона должна быть больше скорости света. Спин есть специфическая квантовомеханическая величина, не имеющая никаких классических аналогов и только по своим формальным свойствам совпадающий с некоторым моментом импульса. Важно сознавать также, что орбитальный момент - характеристика состояния частицы (грубо говоря, определяется ее движением), а спин не зависит от состояния. Это есть ее внутренняя, врожденная характеристика, подобная массе или электрическому заряду.
Разовьем общий спиновый формализм. Итак, записываем теперь волновую функцию как
y = y(r,s),
где s - новая, спиновая переменная. На нее действуют спиновые операторы
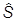 1,
1, 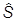 2,
2, 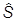 3 и
3 и 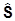 2 =
2 = 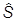 1 2 +
1 2 +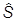 22 +
22 +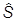 32.
32.
В конце прошлой лекции мы видели, что они должны удовлетворять тем же коммутационным соотношениям, что и операторы момента:
[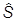 j,
j,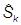 ] = i
] = i ejkl
ejkl 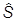 l ; [
l ; [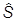 j,
j,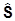 2] =
2] = 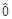 .
.
Поскольку спин - внутренняя характеристика частицы (а не характеристика состояния), то волновую функцию ее нужно снабдить соответствующим индексом, записывая
y = yS(r,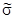 ).
).
Эта функция должна быть собственной для оператора  2(значение спина раз и навсегда фиксировано):
2(значение спина раз и навсегда фиксировано):
 2yS(r,
2yS(r,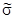 ) =
) =  2s(s+1) yS(r,
2s(s+1) yS(r,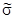 ),
),
где S - полуцелое или целое число (значение его определяется типом частицы). В качестве базисных элементов в пространстве спиновых переменных можно выбрать собственные векторы оператора 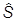 3 - проекции спина (тем самым, эта наблюдаемая наряду с координатами включается в полный набор):
3 - проекции спина (тем самым, эта наблюдаемая наряду с координатами включается в полный набор):
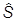 3ySs(r,
3ySs(r,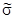 ) =
) = 
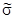 ySs (r,
ySs (r,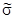 )
)
Значения 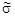 меняются через 1 в интервале
меняются через 1 в интервале
-s £ 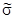 £ s,
£ s,
и всего имеется 2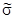 +1 спиновых независимых состояний.
+1 спиновых независимых состояний.
Волновую функцию любого состояния частицы со спином будем записывать в виде матрицы-столбца из 2s+1 строк:
yS(r,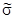 ) =
) =  .
.
Если спиновые и пространственные переменные независимы (отсутствует так называемое спин-орбитальное взаимодействие, ответственное за тонкую структуру спектров), то координатная зависимость у волновой функции будет единой, и ее можно вынести:
yS(r,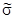 ) = y(r)
) = y(r)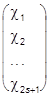 º y(r)cs
º y(r)cs
Матрица - столбец
cs = 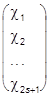
называется спиновой волновой функцией. В общем случае условие нормировки волновой функции yS записывается как
 |yi(r)|2dV = 1.
|yi(r)|2dV = 1.
Смысл каждого слагаемого очевиден: это вероятность обнаружить частицу в данном спиновом состоянии. Если спиновые переменные и координаты расцепляются, то функция y(r) нормируется обычным образом:
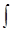 |y(r)|2dV = 1,
|y(r)|2dV = 1,
а спиновая волновая функция нормируется так:
 = 1,
= 1,
где смысл каждого слагаемого тот же. Это условие нормировки можно записать иначе:
(c,c) = c+c = 1,
где c+ - матрица-строка, транспонированная к матрице-столбцу c:
c+ = (c1*,c2*,...c2s+1*).
Спиновую волновую функцию можно записать в виде
c = 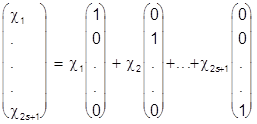 º c1е1 +...cnen,
º c1е1 +...cnen,
где столбики с одной единицей и остальными нулями имеют смысл базисных векторов в спиновом пространстве. Имея в виду, что
(S3)nm = mdnm
(см. выше - в общей теории момента), то матрицей оператора 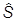 3 в каноническом базисе является
3 в каноническом базисе является
(S3)nm =  .
.
Легко видеть, что каждый из базисных векторов является собственным вектором для этой матрицы, причем собственное значение для него определяется номером места, на котором стоит 1: у е1 оно равно S, у е2 - S-1,...у е2s+1 - равно -S. Поэтому целесообразнее ввести обозначения
cS º |cS ñ =  = cS,S
= cS,S  + cS,S-1
+ cS,S-1 + cS,-S
+ cS,-S º
º
º cS,S |cS,S ñ + cS,S-1 |cS,S-1 ñ + ...+ cS,-S |cS,-S ñ,
где |cS,mS ñ - базисные векторы, описывающие состояния со спином S и его проекцией mS, а cS,mS - числа, т.е. коэффициенты разложения спиновой функции |cSñ по базисным векторам. Величина |cS,mS|2 есть вероятность обнаружить частицу в состоянии с проекцией спина, равной mS . Базис является ортонормированным:
ácS,mS |cS,m¢Sñ = dms,ms¢
и удовлетворяет условию полноты:
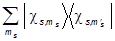 =
=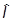 .
.
Все прочие операторы спина, как и 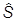 3, изображаются матрицами. Их вид был получен при рассмотрении общей теории момента:
3, изображаются матрицами. Их вид был получен при рассмотрении общей теории момента:
(S1)msms = 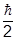
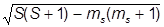 dms,
dms,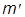 S+1+
S+1+
+
 dm,m¢s-1
dm,m¢s-1
(S2)msms¢¢ = -

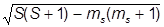 dms,m¢s+1
dms,m¢s+1
+ 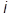
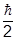
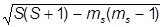 dm,m¢s-1
dm,m¢s-1
(S3) msms¢ = msdms,m¢s, (S2) ms,m¢s =  2S(S+1) dms,m¢s.
2S(S+1) dms,m¢s.
В важнейшем частном случае спина S = 1/2 (электрон, протон, нейтрон и многие другие частицы) волновые функции являются столбцами из двух чисел, а спиновые операторы выражаются через матрицы Паули, как это было показано в самом конце общей теории. Отметим следующие свойства матриц Паули:
1. Они эрмитовы
sj+ = sj
2. След каждой равен нулю
Sp(sj) = 0,
3. Квадрат каждой матрицы Паули равен единичной матрице
sj2 = 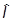 ,
,
4. Разные матрицы Паули антикоммутируют
sjsk + sksj = 0, j ¹ k,
5. Свойства 3 и 4 совместно записываются как
sjsk + sksj = 2djk 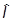 ,
,
6. Матрицы Паули удовлетворяют коммутационным соотношениям
[sj,sk] = 2ejklsl,
7. Произведение двух разных матриц Паули равно (с точностью до множителя) третьей
s1s2 = is3, s3s1 = is2, s2s3 = is1.
СЛОЖЕНИЕ МОМЕНТОВ
Пусть система состоит из двух частей, которым соответствуют полные моменты (1) и (2). Так как эти операторы действуют только на свои переменные, то… [(1), (2)] = ,– Конец работы –
Используемые теги: матрицы, операторов, момента, импульса0.076
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: МАТРИЦЫ ОПЕРАТОРОВ МОМЕНТА ИМПУЛЬСА
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов