рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- СЛОЖЕНИЕ МОМЕНТОВ
Реферат Курсовая Конспект
СЛОЖЕНИЕ МОМЕНТОВ
СЛОЖЕНИЕ МОМЕНТОВ - раздел Математика, МАТРИЦЫ ОПЕРАТОРОВ МОМЕНТА ИМПУЛЬСА Пусть Система Состоит Из Двух Частей, Которым Соответствуют П...
Пусть система состоит из двух частей, которым соответствуют полные моменты  (1) и
(1) и  (2). Так как эти операторы действуют только на свои переменные, то они взаимно коммутируют:
(2). Так как эти операторы действуют только на свои переменные, то они взаимно коммутируют:
[ (1),
(1),  (2)] =
(2)] = 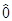 ,
,
причем, между собой операторы каждой группы коммутируют обычным способом:
[ j(a),
j(a), k(a)] = i
k(a)] = i ejkl
ejkl  l(a), [
l(a), [ (a)2,
(a)2, j(a)] =
j(a)] = 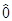 .
.
У полной системы имеются состояния с определенными значениями квадратов моментов 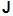 (1)2 и
(1)2 и 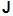 (2)2 и их проекций на третью ось
(2)2 и их проекций на третью ось 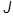 3(1) и
3(1) и 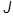 3(2):
3(2):
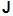 (1)2 =
(1)2 =  2j1(j1+1),
2j1(j1+1), 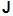 (2)2 =
(2)2 =  2j2(j2+1),
2j2(j2+1), 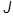 3(1) =
3(1) =  m1, J3(2) =
m1, J3(2) =  m2.
m2.
Эти состояния описываются векторами
|j1m1j2m2ñ = |j1m1ñ|j2m2ñ,
являющимися собственными для каждого из операторов  (1)2,
(1)2,  (2)2,
(2)2, 3(1) и
3(1) и  3(2) с указанными собственными значениями. Эти векторы образуют базис в пространстве состояний полной системы, и по нему можно разложить произвольный вектор ее состояния:
3(2) с указанными собственными значениями. Эти векторы образуют базис в пространстве состояний полной системы, и по нему можно разложить произвольный вектор ее состояния:
|yñ =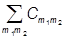 |j1m1j2m2ñ, Cm1Cm2 = áj1m1j2m2|yñ.
|j1m1j2m2ñ, Cm1Cm2 = áj1m1j2m2|yñ.
Введем оператор полного момента
 =
= (1)+
(1)+ (2).
(2).
Для него справедливы обычные коммутационные соотношения
[ j,
j, k] = i
k] = i ejkl
ejkl  l, [
l, [ 2,
2, j] =
j] =  .
.
Каждый из введенных базисных векторов будет собственным для оператора
 3 =
3 =  3(1) +
3(1) + 3(2)
3(2)
с собственным значением
J3 =  (m1+m2) º
(m1+m2) º  m.
m.
Действительно,
 3|j1m1j2m2ñ =
3|j1m1j2m2ñ = 3(1)|j1m1j2m2ñ +
3(1)|j1m1j2m2ñ + 3(2)|j1m1j2m2ñ =
3(2)|j1m1j2m2ñ =  m1|j1m1j2m2ñ +
m1|j1m1j2m2ñ +  m2|j1m1j2m2ñ.
m2|j1m1j2m2ñ.
Оператор квадрата полного момента
 2 =
2 =  (1)2 +
(1)2 +  (2)2 + 2
(2)2 + 2 (1)
(1)  (2)
(2)
коммутирует с операторами  (1)2 и
(1)2 и  (2)2, а потому он может иметь определенное значение J2вместе с квадратами моментов каждой из подсистем. Однако, старые векторы не будут собственными для этого оператора из-за наличия в нем третьего слагаемого, которое будет перемешивать состояния с разными m.
(2)2, а потому он может иметь определенное значение J2вместе с квадратами моментов каждой из подсистем. Однако, старые векторы не будут собственными для этого оператора из-за наличия в нем третьего слагаемого, которое будет перемешивать состояния с разными m.
Но можно всегда построить новый базис из векторов
|j1j2jmñ,
которые являются собственными для  2 и
2 и  3:
3:
 2|j1j2jmñ =
2|j1j2jmñ =  2j(j +1) |j1j2jmñ,
2j(j +1) |j1j2jmñ, 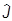 3|j1j2jmñ =
3|j1j2jmñ =  m|j1j2jmñ,
m|j1j2jmñ,
т.е. описывают состояния с определенными j1,j2 (это всегда), а также с определенными j и m. Как уже говорилось, любые векторы, а значит и эти, можно разложить по старому базису:
|j1j2jmñ =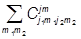 |j1m1j2m2ñ,
|j1m1j2m2ñ, 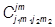 áj1m1j2m2|j1j2jmñ.
áj1m1j2m2|j1j2jmñ.
Возникающие здесь важные числа C......называются коэффициентами Клебша-Гордона, причем фазовые множители у новых базисных векторов всегда можно выбрать так, чтобы эти коэффициенты были вещественными. Для них имеются общие формулы, но они очень сложны. Поэтому существуют специальные таблицы коэффициентов Клебша-Гордона (ККГ).
ККГ задают матрицу преобразования от представления, в котором заданы проекции моментов подсистем (и их моменты) к представлению, в котором задан полный момент и его проекция (и моменты подсистем). Эта матрица осуществляет переход от одного ортонормированного базиса к другому, а потому она унитарна:
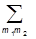 áj1m1j2m2|jmñáj1m1j2m2|jm¢ñ = djj¢dmm¢
áj1m1j2m2|jmñáj1m1j2m2|jm¢ñ = djj¢dmm¢
или
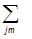 áj1m1j2m2|jmñáj1m1¢j2m2¢|jmñ = dm1m¢1dm2m¢2.
áj1m1j2m2|jmñáj1m1¢j2m2¢|jmñ = dm1m¢1dm2m¢2.
Обратный переход осуществляется обратной матрицей, которая в силу унитарности, равна эрмитово сопряженной матрице, а в силу вещественности - просто транспонированной к исходной матрице:
|j1m1j2m2ñ = 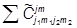 |j1j2jmñ,
|j1j2jmñ,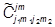 = áj1j2jm|j1m1j2m2ñ.
= áj1j2jm|j1m1j2m2ñ.
Мы уже установили, что каждый старый вектор |j1m1j2m2ñ является собственным для оператора  3 с собственным значением
3 с собственным значением
J3 =  (m1+m2).
(m1+m2).
Поэтому
m = m1+m2
и суммирование в разложении ККГ по одному из индексов носит формальный характер. Так как m2=m-m1, то при заданном m суммирование можно вести только по m1. Это отвечает тому, что
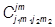 ~ dm,m1+m2.
~ dm,m1+m2.
Важная задача - определение возможных значений j при заданных j1 и j2. Для ее решения исследуем возможные значения m. Его максимальное значение есть m=j1+j2 . Оно осуществляется в одном единственном состоянии |j1j1ñ|j2j2ñ, которое будет иметь
j = j1 + j2.
Следующее значение m=j1+j2-1 может осуществляться двумя линейными комбинациями векторов
|j1,j1-1ñ|j2,j2ñ и |j1,j1ñ|j2,j2-1ñ.
Одна из них отвечает уже найденному моменту j=j1+j2 ( вектор торчит несколько «вбок»), а другая - значению
j = j1 + j2 - 1
(вектор направлен по оси). Значению m=j1+j2-2 будут отвечать три линейные комбинации из трех векторов
|j1,j1-2ñ|j2j2ñ, |j1,j1-1ñ|j2,j2-1ñ, |j1,j1ñ|j2,j2-2ñ.
Одна отвечает значению j=j1+j2 (еще больше вбок), другая - значению j=j1+j2-1 (немножко вбок) и третья - значению
j = j1 + j2 - 2
(вдоль оси). Продолжая процесс, убедимся, что на каждом этапе, когда m уменьшается на 1, появляется новое значение j до тех пор, пока не дойдем до значений, при которых либо m1=-j1, либо m2 =-j2. Таким образом, минимальное значение есть
j = (j1 - j2).
Итак, получаем следующее правило сложения моментов импульса: при заданных значениях j1 и j2 квантовое число j может пробегать множество значений через 1 из интервала
|j1-j2| £ j £ j1 + j2.
Каждому j отвечает 2j+1 состояний, а потому всего их будет
 = (2j1 + 1)(2j2 + 1)
= (2j1 + 1)(2j2 + 1)
(сумма арифметической прогрессии). Это совпадает с числом «старых» состояний |j1m1ñ|j2m2ñ, которое очевидным образом равно (2j1+1)(2j2+1). Конечно, так и должно быть, и совпадение подтверждает правильность найденного правила сложения моментов. Полученные неравенства допускают простую геометрическую интерпретацию - как неравенства для сторон треугольника. Поэтому их называют соотношением треугольника и кратко записывают как D(j j1 j2). Числа j, j1, j2 входят в соотношение треугольника симметрично. Если они не выполняются, то ККГ автоматически обращаются в нуль.
В качестве операторов  (1) и
(1) и  (2) можно рассматривать операторы орбитального момента
(2) можно рассматривать операторы орбитального момента  и спинового момента
и спинового момента 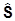 - ведь важно лишь то, что разные операторы коммутируют друг с другом, а для
- ведь важно лишь то, что разные операторы коммутируют друг с другом, а для  и
и 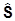 это так. В частности, очень важен случай S = 1/2 (электрон). Если l ¹ 0, то полный момент j может принимать два значения:
это так. В частности, очень важен случай S = 1/2 (электрон). Если l ¹ 0, то полный момент j может принимать два значения:
l+1/2 и l-1/2.
Но в S- состоянии, когда l = 0 , полный момент равен 1/2, и только. Таким образом, получаем следующие возможные состояния электрона:
s1/2; p1/2; p3/2; d3/2; d5/2;...
Всего таких состояний имеется:
s-2, p-2+4 = 6, d-4+6=10,...
Число же низших состояний таково:
s-2, s, p-8, s, p, d-18,...
Очень похоже на числа заполнения в таблице Менделеева, и недаром. Ведь в атоме при n=2 есть s- и p- состояния, откуда - 8, при n= 3 есть s-, p- и d- состояния, откуда - 18, т.д.
При сложении орбитального момента электрона с его спином полезно знать соответствующие разложения. Поэтому приведем таблицу ККГ:
| ms = +1/2 | ms = -1/2 | |
| j = l + 1/2 | 
| 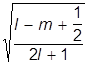
|
| j = l – 1/2 | 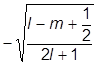
| 
|
Запишем также для справок волновые функции электрона в центральном
поле, где сохраняются  и
и 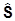 :
:
s = 1/2, ms = +1/2, -1/2,
l, ml = m-ms
Разложение волновой функции состояния с определенными значениями энергии, орбитального момента l (спина s), полного момента j и его проекции m по состояниям с определенными значениями 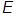 , l, ml, s, ms имеет вид
, l, ml, s, ms имеет вид
yElsjm( r ,s)=  ,
,
где  - спиновая переменная, а
- спиновая переменная, а  - спиновые функции. Разложение можно записать короче:
- спиновые функции. Разложение можно записать короче:
yElsjm( r ,s) = 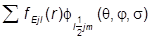
где f - сферические функции со спином (шаровые функции):
 ;
;
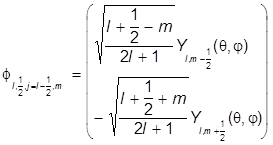 .
.
– Конец работы –
Эта тема принадлежит разделу:
МАТРИЦЫ ОПЕРАТОРОВ МОМЕНТА ИМПУЛЬСА
МАТРИЦЫ ОПЕРАТОРОВ МОМЕНТА ИМПУЛЬСА... Мы хотим найти матрицы спиновых операторов в явном виде Для этого решим сначала более общую задачу найдем матрицы...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: СЛОЖЕНИЕ МОМЕНТОВ
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов