Геометрический смысл несобственного интеграла

Если 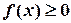, то несобственный интеграл выражает площадь неограниченной (бесконечной) области, заключенной между линиями 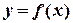, и осью абсцисс (рис. 1).

 

 

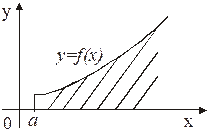
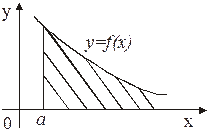
а) б)

Рис. 1

На рисунке 1 (а) представлен случай, когда - сходится, а в случае (б) – расходится.

 

2. Несобственные интегралы от разрывных функций (II рода)

 

Пусть функция 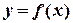непрерывна при , а в точке х = b имеет разрыв (рис. 2). В этом случае при любом разбиении отрезка 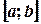на части 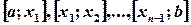функция f(х) будет неограниченной на последнем отрезке. Поэтому, если взять точку 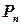достаточно близко к точке b, то можно сделать произведение 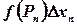, а следовательно, и интегральную сумму , сколь угодно большими.

 

 

 

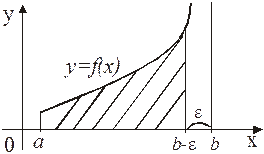
Рис. 2

Это значит, что интегральные суммы неограниченны и они не имеют конечного предела при стремлении шага разбиения к нулю, т.е. прежнее определение интеграла неприменимо.

Однако и в этом случае можно обобщить понятие интеграла.

Рассмотрим отрезок 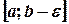, где 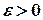, на котором функция f(х) непрерывна.

Определение. Если существует конечный предел определенного интеграла

при 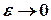, то этот предел называется несобствен-

ныминтегралом II родаот разрывной функции и обознача-

ется символом .

Следовательно, 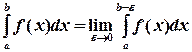. (4)

 

Если предел, стоящий в правой части равенства (4) существует и конечен, то несобственный интеграл называется сходящимся. Если же указанный предел не существует, то говорят, что интеграл расходится.

Аналогично, если f(х ) разрывна в некоторой внутренней точке х = с

отрезка 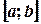, то необходимо разбить этот отрезок на два: 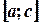и .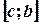

Если несобственные интегралы от данной функции существуют на каждом промежутке, то сумма этих интегралов, по определению, называется несобственным интегралом от функции f(х) на отрезке 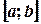, т.е.

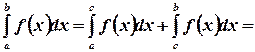
. (5)

Если хотя бы один из несобственных интегралов, стоящих в правой части равенства (5) не существует, то несобственный интеграл называется расходящимся.

Таким образом, из данных определений видно, что несобственный интеграл от разрывной функции является не пределом интегральных сумм, а пределом определенного интеграла.

 

Пример 2. Вычислить несобственный интеграл или установить его расходимость: а) ; б).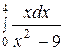

Решение.

а) Подынтегральная функция 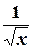непрерывна на отрезке интегрирования , кроме точки х = 0, где она терпит разрыв второго рода. Тогда, по определению, имеем: . Следовательно, данный интеграл сходится.

 

б) Подынтегральная функция не существует, если . Так как х = 3 является внутренней точкой отрезка интегрирования 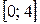, то согласно формуле (3), получаем: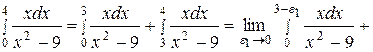

.

 

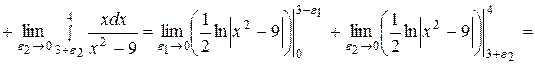
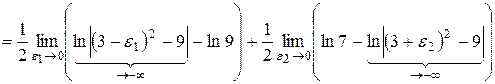Так как оба несобственных интеграла расходятся, то расходится и исходный интеграл.