Движение к экстремуму методом крутого восхождения.
Движение к экстремуму осуществляется по направлению градиента (антиградиента) функции отклика у.
Вектор градиента определяет направление наискорейшего возрастания функции и для
 равен:
равен:
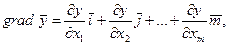 где
где
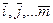 - единичные векторы в направлении осей координат;
- единичные векторы в направлении осей координат;
 - проекции вектора градиента на оси координат
- проекции вектора градиента на оси координат 
Для m = 2 движение методом крутого восхождения можно представить:

 - центры планов эксперимента первого порядка (ПФЭ)
- центры планов эксперимента первого порядка (ПФЭ)
 - центр плана эксперимента второго порядка (ОЦКП)
- центр плана эксперимента второго порядка (ОЦКП)
Последовательные координаты поиска экстремума в факторном пространстве определяются по формуле:
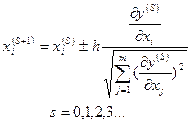 , где
, где
h - задаваемый фактор шага по направлению вектора-градиента;
s - номер точки экспериментирования;
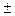 - движение к максимуму (+) или к минимуму (-);
- движение к максимуму (+) или к минимуму (-);
Величина y здесь определяется из уравнения регрессии, которое является линейным относительно факторов и коэффициентов:

Это уравнение используется для локального описания поверхности отклика в областях, далёких от её экстремального значения.
Ограниченная область факторного пространства, где справедливо это уравнение регрессии, задаётся центром области 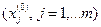 – центром плана эксперимента:
– центром плана эксперимента:
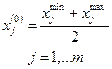
и интервалом (точнее, полуинтервалом) варьирования факторов:

Для локальной области факторного пространства уравнение регрессии записывается с кодированными факторами:
 где
где
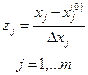
В результате минимальному значению фактора соответствует zj = -1, максимальному - zj = 1, а центру плана эксперимента – точка с координатами zj = 0, j = 1, …m
Коэффициенты уравнения регрессии с кодированными факторами  отличаются от коэффициентов уравнения регрессии с натуральными значениями факторов xj и определяются из полного факторного эксперимента (ПФЭ), проведённого в рассматриваемой ограниченной области.
отличаются от коэффициентов уравнения регрессии с натуральными значениями факторов xj и определяются из полного факторного эксперимента (ПФЭ), проведённого в рассматриваемой ограниченной области.
Одним из таких свойств является свойство ротатабельности, которое характеризует равную предсказательную способность уравнения регрессии с кодированными факторами на одинаковом расстоянии от центра плана.
Для характеристики предсказательной способности уравнения регрессии используется оценка дисперсии выходной переменной  , которая из-за статистической независимости коэффициентов
, которая из-за статистической независимости коэффициентов  и их одинаковой дисперсии в случае ПФЭ определяется по формуле:
и их одинаковой дисперсии в случае ПФЭ определяется по формуле:
 где
где
 - одинаковая для всех коэффициентов оценка дисперсии
- одинаковая для всех коэффициентов оценка дисперсии  ,
,
 где
где
n - число опытов ПФЭ
 - дисперсия воспроизводимости выходной переменной у , определяемая по параллельным опытам
- дисперсия воспроизводимости выходной переменной у , определяемая по параллельным опытам
ρ2 - квадрат расстояния из центра плана до рассматриваемой точки факторного пространства:
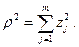
Величина, обратная  , принимается за меру точности уравнения регрессии.
, принимается за меру точности уравнения регрессии.
Точность уравнения для  убывает пропорционально квадрату радиуса сферы ρ2 и одинакова для всех эквидистантных точек.
убывает пропорционально квадрату радиуса сферы ρ2 и одинакова для всех эквидистантных точек.
Поэтому в факторном пространстве нельзя выделить ни одно предпочтительное направление, и вектор градиента (  )не хуже, в смысле предсказания величины выходной переменной у , чем любое другое направление.
)не хуже, в смысле предсказания величины выходной переменной у , чем любое другое направление.
Однако вектор-градиент (  ) характеризует направление наискорейшего возрастания функции у и в этом смысле движение по нему является наиболее предпочтительным.
) характеризует направление наискорейшего возрастания функции у и в этом смысле движение по нему является наиболее предпочтительным.
Для определения координат вектора-градиента (  ) используется адекватное уравнение регрессии, полученное по результатам ПФЭ:
) используется адекватное уравнение регрессии, полученное по результатам ПФЭ:
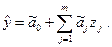
Задаётся фактор шага h , и из центра плана ПФЭ ( - начальное приближение) выполняется шаг по градиенту в сторону экстремального значения функции отклика, определяются координаты нового центра плана в факторном пространстве -
- начальное приближение) выполняется шаг по градиенту в сторону экстремального значения функции отклика, определяются координаты нового центра плана в факторном пространстве -  .
.
Здесь снова проводится ПФЭ, обрабатываются его результаты, вычисляется новое направление вектора-градиента:
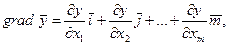
по которому выполняется шаг
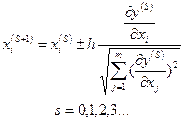
в сторону экстремума. Процедура последовательного экспериментирования продолжается до тех пор, пока не будет достигнута область, близкая к экстремальному значению функции отклика.
Близость почти стационарной области может быть установлена с помощью t – критерия Стьюдента путём оценки значимости различия между экспериментальными  и расчётными
и расчётными  величинами в центре плана.
величинами в центре плана.


Условие близости экстремума функции отклика имеет вид:
 где
где
fe = k – 1 - число степеней свободы
k - число параллельных опытов
β - заданная доверительная вероятность (обычно 0,95)