Основные методы интегрирования. - Лекция, раздел Математика, Раздел 2. Дифференциальное исчисление. Дифференциальные уравнения. Ряды 1) Непосредственное Интегрирование;
2) Метод Подстановки;
3...
1) Непосредственное интегрирование;
2) Метод подстановки;
3) Метод интегрирования по частям.
1) Непосредственное интегрирование. Вычисление интегралов с помощью таблицы простейших интегралов и основных свойств неопределённых интегралов называется непосредственным интегрированием.
2) Метод подстановки. Во многих случаях введение новой переменной интегрирования позволяет свести нахождение данного интеграла к нахождению табличного, т. е. перейти к непосредственному интегрированию. Такой метод называется методом подстановки или методом замены переменной. В его основе лежит следующая теорема.
Теорема:Пусть функция x=j(t) определена и дифференцируема на некотором промежутке Т и пусть X - множество значений этой функции, на котором определена функция f(x), т. е. на Т определена сложная функция f(j(t)). Тогда если на множестве X функция f(x) имеет первообразную F(x), то справедлива формула (формула замены переменной в неопределённом интеграле):

Тождественное преобразование подынтегрального выражения с выделением дифференциала новой переменной интегрирования – простейшая замена переменной или метод внесения под знак дифференциала. Таким образом, устанавливается и общая формула
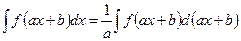
3) Метод интегрирования по частям. Метод интегрирования по частям основан на использовании формулы дифференцирования произведения двух функций.
Теорема:Пусть функции u(х) и v(x) определены и дифференцируемы на некотором промежутке X и пусть функция u'(x)v(x) имеет первообразную на этом промежутке, т. е. существует òv(x)u'(x)dx. Тогда на промежутке X функция u(x)v'(x) также имеет первообразную и справедлива формула:
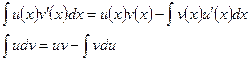
Интегрирование сложнее дифференцирования. Дифференцирование не выводит из класса элементарных функций в отличие от интегрирования.
Все темы данного раздела:
Первообразная
Восстановление функции по известной производной этой функции составляет одну из основных задач интегрального исчисления.
Определение 1:
Неопределённый интеграл.
Определение 1:Если функция F(x) — первообразная для функции f(x), то множество функций F(x)+C, где С — произвольн
Свойства неопределённого интеграла.
Свойство 1:Производная неопределённого интеграла равна подынтегральной функции; дифференциал от неопределённого интеграла равен подынтегральному выражени
Основные свойства неопределённого интеграла.
Производная неопределённого интеграла равна подынтегрально
Основные методы интегрирования.
Непосредственное интегрирование
Вычисление интегралов с помощью таблицы простейших интегралов и основных свойств неопределённых интегралов.
Метод
Основные свойства определённого интеграла.
Если а=b, то
Если а>b, то
Интегрирование рациональных функций.
Интегралы от рациональных функций всегда выражаются через элементарные функции.
Задача интегрирования рациональной функции сводится к нахождению интегралов следующих четырёх типов:
Интегрирование некоторых тригонометрических выражений.
· Для нечётных степеней sinx или cosx применимо правило:
Правило 1:
Для вычисления интегралов вида:
Некоторые интегралы, зависящие от радикалов.
Символ R(x; y) здесь и в дальнейшем обозначает дробь, числитель и знаменатель которой – многочлены относительно букв х, у. Такая дробь называется рациональной фун
Подстановки Эйлера.
Интегралы вида:
рационализируются одной из подстановок Эйлера:
Определённый интеграл.
Пусть функция y=f(x) определена на отрезке [а, b], а<b. Разобьем этот отрезок на n произвольных частей точками а=x0<x1
Основные свойства определённого интеграла.
· Если а=b, то ;
· Если а>b, то
Формула Ньютона Лейбница.
Теорема (Основная теорема интегрального исчисления):Пусть функция f(x) непрерывна на отрезке [а, b]. Тогда, если функция F(x) является некоторой
Несобственные интегралы.
Определение 1: Определённый интеграл , где промежуток интег
Интеграл с бесконечным промежутком интегрирования
(несобственный интеграл I рода)
Пусть функция f(x) непрерывна на промежутке [а, +¥). Если существует конечный предел
Интеграл функции, имеющей разрыв
(несобственный интеграл II рода)
Пусть функция f(x) имеет разрыв в точке х=b, а остальных точках этого промежутка (а; b) она непр
Понятие числового ряда.
Пусть дана числовая последовательность а1, а2, а3, ..., аn, ... Выражение вида
Свойства сходящихся рядов.
· Если сходится ряд: , то сходится и ряд:
Достаточные признаки сходимости положительных рядов
Необходимое и достаточное условие сходимости положительного ряда:Для того чтобы ряд
Знакопеременный ряд. Признак Лейбница
Ряд называется знакопеременным, если его члены поочерёдно положительны и отрицательны:
Абсолютная и условная сходимость
Ряд (1) (с членами произвольных знаков) заведомо сходится, если сходится положительный
Ответ: ряд сходится.
·
Применим признак сравнения:
Сравним данный ряд с
Степенной ряд.
Стеленным рядом называется ряд вида (1): ао+а1х+а2х2+...+апхп+...,
а также ряд более общего вида (2): а
Промежуток и радиус сходимости степенного ряда, расположенного по степеням х
Теорема 1. Область сходимости степенного ряда есть некоторый промежуток (-R, R), симметричный относительно точки х=0. Иногда в него надо
Промежуток и радиус сходимости степенного ряда, расположенного по степеням х-а
Теорема 1. Область сходимости степенного ряда, расположенногопо степеням х-а есть некоторый промежуток (а-R, а+R), симметричный относитель
Разложение функций в степенной ряд
Разложить функцию f(x) в степенной ряд, расположенный по степеням х - х0 – это значит составить ряд, у которого радиус сходимости не равен нулю, а сумма тождественно равна данной
Дифференциальные уравнения первого порядка
Определение 1.Уравнение вида F(x, y, y')=0, где х — независимая переменная; у — искомая функция; у' — ее производная, называется дифференциальным уравнением
Лекция 5
§94 Линейное ДУ I порядка (ЛДУ I)
Пусть ДУ I имеет вид: Мdx+Ndy=0 – оно называется ЛДУ I, если отношение M/N сод
Метод Бернулли.
Решение уравнения у¢+Р(x)у=Q(x) ищется в виде произведения двух других функций, то есть с помощью подстановки y=u·v, где u(x) и v(x) – неизвестные функции от х, причём одна из них произвольна,
Метод Лагранжа (метод вариации постоянной).
Решение уравнения у¢+Р(x)у=Q(x) ищется в следующей последовательности:
Составим вспомогательное ЛОДУ I у¢+Р(x)у=0 и решим его как уравнение с разделяющимися переменными. То есть
ЛОДУ II с постоянными коэффициентами.
ау²+bу¢+cу=0, где а, b, c – некоторые постоянные.
Составим характеристическое уравнение аk2+bk+
ЛНДУ II с постоянными коэффициентами.
ау²+bу¢+cу=R(x), где а, b, c – некоторые постоянные.
Его общее решение имеет вид:
Свойства сходящихся рядов.
· Если сходится ряд: , то сходится и ряд:
Достаточные признаки сходимости положительных рядов
Необходимое и достаточное условие сходимости положительного ряда:Для того чтобы ряд
Знакопеременный ряд. Признак Лейбница
Ряд называется знакопеременным, если его члены поочерёдно положительны и отрицательны:
Степенной ряд.
Степенным рядом называется ряд вида (1): ао+а1х+а2х2+...+апхп+...,
а также ряд более общего вида (2): а
Расположенного по степеням х
Теорема Область сходимости степенного ряда, расположенного по степеням х есть (-R, R), симметричный относительно точки х=0. Иногд
Расположенного по степеням х-а
Теорема Область сходимости степенного ряда, расположенного по степеням х-а есть некоторый промежуток (-R+а R+а), симметричный отн
Дифференциальные уравнения первого порядка
Уравнение вида F(x, y, y')=0, где х — независимая переменная; у — искомая функция; у' — её производная, называется дифференциальным уравнением первого порядка.
Метод Бернулли.
Решение уравнения у¢+Р(x)у=Q(x) ищется в виде произведения двух других функций, то есть с помощью подстановки y=u·v, где u
Метод Лагранжа (метод вариации постоянной).
Решение уравнения у¢+Р(x)у=Q(x) ищется в следующей последовательности:
Составим вспомогательное ЛОДУ−I у¢+Р(x
ЛОДУ−II с постоянными коэффициентами.
ау²+bу¢+cу=0, где а, b, c – некоторые постоянные.
Составим характеристическое уравнение аk2+bk+c=0, кото
ЛНДУ−II с постоянными коэффициентами.
ау²+bу¢+cу=R(x), где а, b, c – некоторые постоянные.
Его общее решение имеет вид:

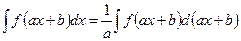
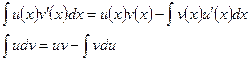







Новости и инфо для студентов