Основные методы интегрирования.
1) Непосредственное интегрирование;
2) Метод подстановки;
3) Метод интегрирования по частям.
1) Непосредственное интегрирование. Вычисление интегралов с помощью таблицы простейших интегралов и основных свойств неопределённых интегралов называется непосредственным интегрированием.
2) Метод подстановки. Во многих случаях введение новой переменной интегрирования позволяет свести нахождение данного интеграла к нахождению табличного, т. е. перейти к непосредственному интегрированию. Такой метод называется методом подстановки или методом замены переменной. В его основе лежит следующая теорема.
Теорема:Пусть функция x=j(t) определена и дифференцируема на некотором промежутке Т и пусть X - множество значений этой функции, на котором определена функция f(x), т. е. на Т определена сложная функция f(j(t)). Тогда если на множестве X функция f(x) имеет первообразную F(x), то справедлива формула (формула замены переменной в неопределённом интеграле):

Тождественное преобразование подынтегрального выражения с выделением дифференциала новой переменной интегрирования – простейшая замена переменной или метод внесения под знак дифференциала. Таким образом, устанавливается и общая формула
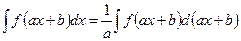
3) Метод интегрирования по частям. Метод интегрирования по частям основан на использовании формулы дифференцирования произведения двух функций.
Теорема:Пусть функции u(х) и v(x) определены и дифференцируемы на некотором промежутке X и пусть функция u'(x)v(x) имеет первообразную на этом промежутке, т. е. существует òv(x)u'(x)dx. Тогда на промежутке X функция u(x)v'(x) также имеет первообразную и справедлива формула:
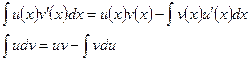
Интегрирование сложнее дифференцирования. Дифференцирование не выводит из класса элементарных функций в отличие от интегрирования.