Дифференциальные уравнения первого порядка

Уравнение вида F(x, y, y')=0, где х — независимая переменная; у — искомая функция; у' — её производная, называется дифференциальным уравнением первого порядка.

Если уравнение можно разрешить относительно у', то оно принимает вид: y'=f(x, y) и называется уравнением первого порядка, разрешенным относительно производной.

Дифференциальное уравнение удобно записать в виде: 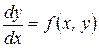, являющемся частным случаем более общего уравнения (в симметрической форме): P(x,y)dx+Q(x, y)dy =0, где Р(x, y) и Q (x, y) — известные функции.

Уравнение в симметричной форме удобно тем, что переменные х и у в нем равноправны, т.е. каждую из них можно рассматривать как функцию от другой.

Решением дифференциального уравнения первого прядка называется функция у=j(х), которая при подстановке в уравнение обращает его в тождество.

График решения дифференциального уравнения называется интегральной кривой.

Общим решением уравнения в некоторой области G плоскости Оху называется функция у=j(х, С), зависящая от х и произвольной постоянной С, если она является решени­ем уравнения при любом значении постоянной С, и если при любых начальных условиях таких, что (х₀; у₀)ÎG, существует единственное значение постоянной С=С₀ такое, что функция у=j(х, С₀) удовлетворяет данным начальным условиям j (х₀, С)=С₀.

Частным решением уравнения в области G называется функция у=j(х, С₀), которая получается из общего решения у=j(х, С) при определенном значении постоянной С=С₀.