Определение производной функции.

Приращение – это величина, на которую увеличивается переменная величина.

Пусть на некотором промежутке X определена функция y=f(x).

Проделаем следующие действия:

· возьмем любую точку х₀ÎХ и зададим аргументу х в точке х₀ произвольное приращение Dх такое, что точка х₀+Dх также принадлежит X или х=х₀+Dх;

· функция получит приращение Dу=f(х₀+Dх)-f(x₀) или Dу=f(х)-f(x₀);

· составим отношение приращения функции к приращению аргумента;

· найдём предел этого отношения при Dх®0;

Определение 1: Производной функции у=f(x) в точке х₀ называется предел при Dх®0 отношения приращения функции в этой точке к приращению аргумента (при условии, что этот предел существует):

Определение 2: Функция y=f(x) называется дифференцируемой в точке х₀, если её приращение Dy в этой точке можно представить в виде Dy=АDх+a(Dх)Dх,

где А - некоторое число, не зависящее от Dх, а a(Dх) - функция аргумента Dх, являющаяся бесконечно малой при Dх®0, т. е. 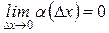. Доказано, что А=f¢(х₀).

Например: у=х³: Dy=(х₀+Dх)³-х₀³=3х²Dх+3х(Dх)²+(Dх)³, где А=3х², не зависящее от Dх, а a(Dх)=3хDх+(Dх)² - функция аргумента Dх, являющаяся бесконечно малой при Dх®0, т. е. .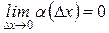

Установим связь между дифференцируемостью функции в точке и существованием производной в той же точке.

Теорема 1: Для того чтобы функция y=f(x) была дифференцируема в точке х₀, необходимо и достаточно, чтобы она имела в этой точке конечную производную.

Таким образом, для функций одной переменной дифференцируемость и существование производной - понятия равносильные. Поэтому операцию нахождения производной часто называют дифференцированием.

Теорема 2:Если функция y=f(x) дифференцируема в данной точке х₀, то она и непрерывна в этой точке.

Замечание. Обратное утверждение неверно. Функция может быть непрерывной в точке, но не быть дифференцируемой, т. е. не иметь производной в этой точке.