рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Формула Тейлора
Реферат Курсовая Конспект
Формула Тейлора
Формула Тейлора - раздел Математика, ГЛАВА 2. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ Формула Тейлора Является Одной Из Важнейших Формул Математического Анализа, О...
Формула Тейлора является одной из важнейших формул математического анализа, она имеет очень большое число теоретических и практических применений.
Рассмотрим предварительно следующую задачу: данный многочлен Pn(x) степени n разложить по степеням разности (x – x0) (где x0 – некоторое число), т.е. представить Pn(x) в виде:
Pn(x) = a0 + a1(x – x0) + a2(x – x0)2 +...+ an(x – x0)n. (2.19)
Вычислим коэффициенты: a0, a1, ..., an. Для этого найдем сначала производные от Pn(x):
 (x) = a1 + 2a2(x – x0) + 3a3(x – x0)2 + ... + n×an(x – x0)n–1;
(x) = a1 + 2a2(x – x0) + 3a3(x – x0)2 + ... + n×an(x – x0)n–1;
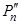 (x) = 2a2 + 2×3a3(x – x0) + 3×4a4(x – x0)2 + ... + (n – 1) ×n×an(x – x0)n–2;
(x) = 2a2 + 2×3a3(x – x0) + 3×4a4(x – x0)2 + ... + (n – 1) ×n×an(x – x0)n–2;
 (x) = 2×3×a3 + 2×3×4a4(x – x0) + ... + (n – 2)(n – 1)×n×an(x – x0)n–3;
(x) = 2×3×a3 + 2×3×4a4(x – x0) + ... + (n – 2)(n – 1)×n×an(x – x0)n–3;
...; Pn(n)(x) = 1×2×...× (n – 1)×n×an; Pn(n+1)(x) = 0. (2.20)
Полагая в равенствах (2.19), (2.20) x = x0, получим:
Pn(x0) = a0,  (x0) = a1,
(x0) = a1,  (x0) = 2a2,
(x0) = 2a2,  (x0) = 2×3a3, ..., Pn(n)(x0) = 1×2×...(n – 1)×n×an,
(x0) = 2×3a3, ..., Pn(n)(x0) = 1×2×...(n – 1)×n×an,
откуда находим:
a0 = Pn(x0), a1 =  (x0), a2 =
(x0), a2 = 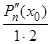 , a3 =
, a3 = 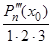 , ..., an =
, ..., an = 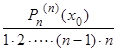 .
.
Подставляя найденные значения a0, a1, ..., an в равенство (2.19), получим разложение многочлена Pn(x) по степеням (x – x0):
Pn(x) = Pn(x0) +  (x – x0) +
(x – x0) + 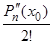 (x – x0)2 + ... +
(x – x0)2 + ... +  (x – x0)n. (2.21)
(x – x0)n. (2.21)
Формула (2.21) называется формулой Тейлора для многочлена Pn(x) n-й степени.
Пусть функция f(x) имеет производные до (n + 1)-го порядка включительно в некотором промежутке, и число x0 принадлежит этому промежутку.
Поставим задачу: найти многочлен n-й степени Pn(x), такой, чтобы значение Pn(x0) совпадало с f(x0), а значение всех производных для Pn(x) в точке x0 (до n-го порядка) совпадало со значениями соответствующих производных для f(x) в точке x0, т.е.
Pn(x0) = f(x0),  (x0) =
(x0) =  (x0),
(x0),  (x0) =
(x0) =  (x0), ..., Pn(n)(x0) = f (n)(x0).
(x0), ..., Pn(n)(x0) = f (n)(x0).
Тогда по формуле (3) многочлен Pn(x) имеет вид:
Pn(x) = f(x0) +  (x – x0) +
(x – x0) + 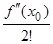 (x – x0)2 + ... +
(x – x0)2 + ... +  (x – x0)n. (2.22)
(x – x0)n. (2.22)
Естественно ожидать, что многочлен Pn(x) будет в некотором смысле «близок» к функции f(x), по крайней мере, около точки x0.
Обозначим: Rn(x) = f (x) – Pn(x), тогда f (x) = Pn(x) + Rn(x). Подставляя вместо Pn(x) его выражение (2.22), получим формулу:
f (x) = f (x0) +  (x – x0) +
(x – x0) + 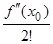 (x – x0)2 +...+
(x – x0)2 +...+ 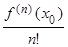 (x – x0)n + Rn(x), (2.23)
(x – x0)n + Rn(x), (2.23)
которая называется формулой Тейлора для функции f(x), а Rn(x) называется остаточным членом.
Если для некоторого x остаточный член Rn(x) достаточно мал, то формула (2.23) дает приближенное значение для f(x): f(x) » Pn(x), при этом погрешность этого приближения равна: Rn(x). Для оценки Rn(x) применяются специальные формулы, одна из них называется формой Лагранжа и имеет вид:
Rn(x) = 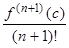 (x – x0)n+1, (2.24)
(x – x0)n+1, (2.24)
где c – некоторое число, заключенное между x0 и x. Число c можно представить в виде:
c = x0 + q(x – x0), где q – некоторое число, заключенное между 0 и 1, т.е. 0 < q < 1. Тогда формула остаточного члена примет вид:
Rn(x) =  (x – x0)n+1, (2.25)
(x – x0)n+1, (2.25)
Другая формула для Rn(x) называется формой Коши и имеет вид:
Rn(x) =  (x – x0)n+1×(1 – q)n, (2.26)
(x – x0)n+1×(1 – q)n, (2.26)
где q удовлетворяет неравенству 0 < q < 1.
Вообще говоря, значения q в формулах (2.25) и (2.26) различные. (Вывод этих формул см. [6, с. 186]).
Заметим, что если в формулах Тейлора (2.23) положить n = 0 и остаточный член записать в форме Лагранжа (2.24), то получим формулу: f(x) = f(x0) +  (c)(x – x0), откуда приходим к формуле Лагранжа: f(x) – f(x0) =
(c)(x – x0), откуда приходим к формуле Лагранжа: f(x) – f(x0) =  (c)(x – x0). Таким образом, формула Тейлора является обобщением формулы Лагранжа (конечных приращений).
(c)(x – x0). Таким образом, формула Тейлора является обобщением формулы Лагранжа (конечных приращений).
Если в формуле Тейлора (2.23) положить x0 = 0, то получится формула, называемая формулой Маклорена:
f(x) = f(0) + 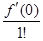 x +
x +  x2 + ... +
x2 + ... +  xn + Rn(x), (2.27)
xn + Rn(x), (2.27)
где Rn(x) = 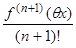 xn+1 – остаточный член в форме Лагранжа (0 < q < 1).
xn+1 – остаточный член в форме Лагранжа (0 < q < 1).
Рассмотрим применение формулы Тейлора. Найдем разложение некоторых элементарных функций по формуле Тейлора, причем возьмем x0 = 0 (т.е. найдем формулы Маклорена для этих функций).
1) f(x) = ex
Так как  (x) = ex,
(x) = ex,  (x) = ex, ..., f (n)(x) = ex и f(0) = 1,
(x) = ex, ..., f (n)(x) = ex и f(0) = 1,  (0) = 1,
(0) = 1,  (0) =1, ...,
(0) =1, ...,
f (n)(0) = 1, то по формуле (2.27) получаем:
ex = 1 + 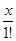 +
+  + ... +
+ ... +  +
+  eqx, 0 < q < 1. (2.28)
eqx, 0 < q < 1. (2.28)
Если |x| £ 1, то при n = 8 получаем: R8 < ×3 <
×3 <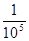 .
.
Пример 1. Вычислить приближенно число e и оценить погрешность.
Решение. Ранее нами было введено число e как предел последовательности:
e =  и установлено, что 2 < e < 3. Используя формулу (2.28), положив x = 1,
и установлено, что 2 < e < 3. Используя формулу (2.28), положив x = 1,
n = 8 имеем: e » 1 + 1 + 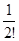 +
+  +
+ 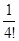 +
+ 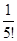 +
+  +
+  +
+ 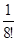 » 2,71828, причем погрешность R8(1) не превосходит 0,00001.
» 2,71828, причем погрешность R8(1) не превосходит 0,00001.
2) f (x) = sinx
Найдем производные до (n + 1)-го порядка для f(x) = sinx и их значения при x= 0:
f(x) = sinx, f(0) = 0,
 (x) = cosx = sin(x +
(x) = cosx = sin(x +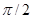 ),
),  (0) = 1,
(0) = 1,
 (x) = –sinx = sin(x + 2×
(x) = –sinx = sin(x + 2×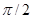 ),
),  (0) = 0,
(0) = 0,
 (x) = –cosx = sin(x + 3×
(x) = –cosx = sin(x + 3×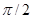 ),
),  (0) = –1,
(0) = –1,
f (4)(x) = sinx = sin(x + 4×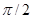 ), f (4)(0) = 0,
), f (4)(0) = 0,
f (n)(x) = sin(x + n×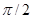 ), f (n)(0) = sin
), f (n)(0) = sin .
.
Если n = 2m, m Î N, то f (2m)(0) = 0; при n = 2m + 1: f (2m+1)(0) = (–1)m, поэтому
sinx = x – 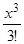 +
+ 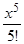 – ... + (–1)m
– ... + (–1)m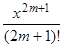 + (–1)m+1
+ (–1)m+1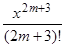 cosqx. (2.29)
cosqx. (2.29)
3) Аналогично для функции f(x) = cosx можно получить следующую формулу Маклорена:
cosx = 1 –  +
+ 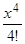 – ... + (–1)m
– ... + (–1)m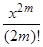 + (–1)m+1
+ (–1)m+1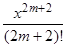 cosqx . (2.30)
cosqx . (2.30)
В последних двух разложениях 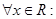 |cosqx| £ 1 и потому Rn(x) по абсолютной величине не превосходит
|cosqx| £ 1 и потому Rn(x) по абсолютной величине не превосходит  (в формуле (2.29)) или
(в формуле (2.29)) или  (в формуле (2.30)).
(в формуле (2.30)).
Пример 2. Вычислить приближенно sin200 с точностью до 0,0001.
Решение.Воспользуемся формулой (2.29), положив x = 200 =  радиан и взяв 2 члена разложения: sin
радиан и взяв 2 члена разложения: sin »
»  –
–  ×
× = 0,3420, |Rn| £
= 0,3420, |Rn| £  ×
×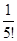 £ 0,0001.
£ 0,0001.
Заданиядля самостоятельной работы.
Вывести формулу Маклорена для функции f (x) = cosx (формулу (2.30)).
Вывести формулу Маклорена для функции f (x) = ln(1+ x).
Вычислить приближенно cos400 и оценить погрешность вычисления, взяв два слагаемых в формуле (2.30).
В следующих разделах мы будем изучать с помощью производных поведение функций. В разд. 2.9 (следствие из теоремы Лагранжа) мы говорили о том, что если производная  (x) = 0 на некотором интервале, то функция f(x) постоянна на этом интервале. Теперь будем изучать другие свойства функции.
(x) = 0 на некотором интервале, то функция f(x) постоянна на этом интервале. Теперь будем изучать другие свойства функции.
– Конец работы –
Эта тема принадлежит разделу:
ГЛАВА 2. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
Основные правила дифференцирования... Установим правила по которым можно находить производные суммы произведения... Теорема Если функции u x v x дифференцируемы в точке x то их сумма дифференцируема в этой точке причем...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Формула Тейлора
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов