Асимптоты

При исследовании функции часто приходится устанавливать вид ее графика (а, значит, и характер функции) при неограниченном удалении точки графика от начала координат (при стремлении переменной точки в бесконечность). При этом важным случаем является тот, когда график функции при удалении его переменной точки в бесконечность неограниченно приближается к некоторой прямой.

Асимптотой графика функции y = f(x) называется такая прямая, что расстояние от переменной точки M на графике до этой прямой стремится к нулю при удалении точки M в бесконечность (рис. 2.17, 2.18).

С примерами асимптот мы встречались при изучении пределов функции (глава 1). Напомним, что если 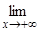f (x) = b, то прямая y = b является асимптотой графика
y = f(x) (при x ® +¥), эта асимптота параллельна оси Ox и называется горизонтальной асимптотой (см. рис. 2.18). Аналогично, прямая y = b является асимптотой графика
y = f(x) при x ® -¥, если f (x) = b (рис. 2.17).

Рассмотрим асимптоты, параллельные оси Oy. Они называются вертикальными асимптотами.

Пусть для функции f (x): f(x) = ¥ или 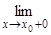f(x) = ¥, тогда из определения асимптоты следует, что прямая x = x₀ - асимптота. Очевидно и обратное, если прямая
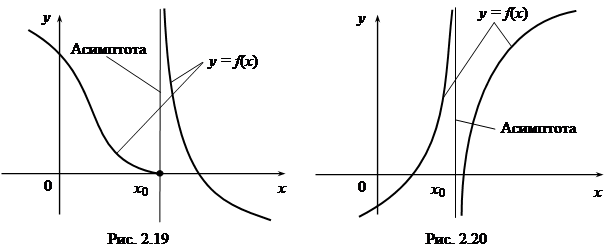
x = x₀ является асимптотой, то хотя бы один из пределов, f(x), 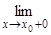f(x), является бесконечным (см. рис. 2.19, 2.20).

Следовательно, для отыскания вертикальных асимптот нужно найти такие значения x₀, односторонние пределы в которых равны бесконечности.

Пример 1. Найти вертикальные асимптоты для графика функции y =.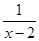

Решение. Функция f(x) = 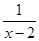определена и непрерывна во всех точках числовой оси, за исключением точки x₀ = 2, в которой функция терпит разрыв,
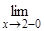
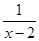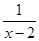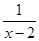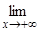
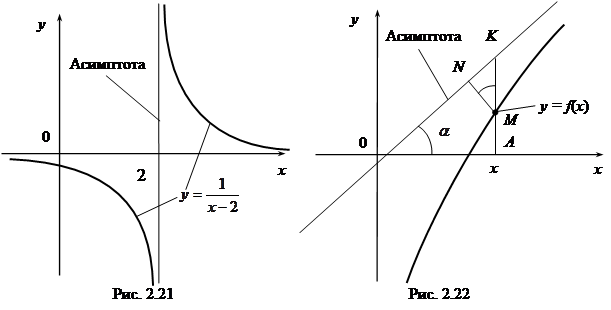
= –¥, = +¥. Следовательно, прямая x = 2 является вертикальной асимптотой для графика y =. Кроме того, = 0 и 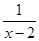= 0, следовательно, прямая y = 0 является горизонтальной асимптотой при x ® +¥ и при x ® -¥ (см. рис. 2.21).

Рассмотрим асимптоты, которые не параллельны оси Oy, будем называть их наклонными асимптотами. Пусть график функции y = f(x) имеет наклонную асимптоту при x ® +¥, тогда ее уравнение имеет вид y = kx + b. Определим числа k и b.

Опустим из точки M(x, f(x)) графика функции перпендикуляр MN на асимптоту (см. рис. 2.22). Из определения асимптоты следует, что при x ® +¥ длина MN ® 0 (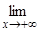MN = 0). Из DMNK имеем MK =, где a – угол наклона асимптоты к оси Ox, поэтому cosa –постоянная величина. Значит, 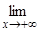MK = 0. Так как MK = |AK – AM|,
AK = kx + b, то MK = |kx + b – f(x)|, следовательно,

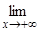(f(x) – kx – b) = 0. (2.31)

Итак, если прямая y = kx + b является асимптотой графика функции y = f (x), то выполняется равенство (2.31) и наоборот, если при постоянных числах k, b выполняется равенство (2.31), то прямая y = kx + b является асимптотой. Из равенства (2.31), разделив бесконечно малую функцию (f(x) – kx – b) на x (а x ® +¥), получим:

= 0, (2.32)

отсюда угловой коэффициент асимптоты:

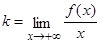. (2.33)

Определим коэффициент b из равенства (2.31), подставив в это равенство значение k:

b = 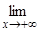(f(x) – kx). (2.34)

Итак, если прямая y = kx + b является асимптотой графика y = f(x), то k, b находятся по формулам (2.33), (2.34). Обратно, если существуют пределы (2.33), (2.34), то прямая y = kx + b есть асимптота. Если хотя бы один из пределов (2.33), (2.34) не существует, то при x ® +¥ кривая не имеет асимптоты.

Аналогично решается вопрос об асимптотах при x ® -¥. Заметим, что отдельно находить горизонтальные асимптоты нет надобности, они будут найдены при нахождении наклонных асимптот (при k = 0).

Пример 2. Найти асимптоты линии y = e^x – x.

Решение. Функция f (x) = e^x – x определена, непрерывна на бесконечном интервале (–¥, +¥), поэтому вертикальных асимптот нет.

Найдем наклонные асимптоты, для этого вычислим пределы (2.33), (2.34) при
x ® +¥, x ® -¥:

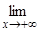
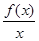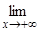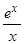= (– 1) = ¥,

так как 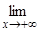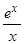= ¥ (проверьте это по правилу Лопиталя). Отсюда следует, что при
x ® +¥ наклонных асимптот нет:

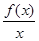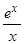= (– 1) = –1, так как 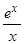= 0,

отсюда k = –1. Далее, (f(x) – kx) = (e^x – x + x) = e^x = 0, значит, b = 0.

Итак, прямая y = –x есть наклонная асимптота при x ® -¥ для графика функции y = e^x – x.

 

 

 

ГЛАВА 2. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ................ 32

2.1. Понятие производной, ее геометрический и механический смысл............................................................................. 32

2.2. Производные некоторых элементарных функций........................................................................................................ 34

2.3. Основные правила дифференцирования....................................................................................................................... 36

2.4. Производные обратных тригонометрических и гиперболических функций.............................................................. 38

2.5. Дифференцирование функций, заданных неявно. Логарифмическое дифференцирование....................................... 39

2.6. Функции, заданные параметрически, и их дифференцирование.................................................................................. 40

2.7. Дифференциал функции................................................................................................................................................ 42

2.8. Производные и дифференциалы высших порядков...................................................................................................... 44

2.9. Основные теоремы о дифференцируемых функциях................................................................................................... 46

2.10. Правило Лопиталя....................................................................................................................................................... 49

2.11. Формула Тейлора....................................................................................................................................................... 51

2.12. Возрастание и убывание функций............................................................................................................................... 54

2.13. Экстремумы функции.................................................................................................................................................. 55

2.14. Выпуклость, вогнутость графика функции, точки перегиба...................................................................................... 58

2.15. Асимптоты................................................................................................................................................................... 60