Доказательство

Так как Du = u(x + Dx) – u(x), то u(x + Dx) = u(x) + Du.

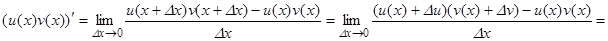Аналогично, v(x + Dx) = v(x) + Dv.

Следствие. Постоянный множитель можно выносить за знак производной, т.е.

(C×f(x))' = C×(x).

Доказательство. Пусть C – постоянное число, тогда (C)' = 0. По теореме 2:

(C×f(x))' = (C)'×f(x) + C×(x) = 0×f(x) + C×(x) = C×(x).

В частности, (u(x) – v(x))' = (u(x) + (–1)×v(x))' = u'(x) + (–1)×v'(x) = u'(x) – v'(x),
т.е. (u(x) – v(x))' = u'(x) – v'(x) (производная разности двух функций равна разности их производных).

Теорема 3. Если функции u(x), v(x) дифференцируемы в точке x и v(x) ¹ 0, то их частное дифференцируемо в этой точке, причем

Доказательство

Заметим, что, так как v(x) дифференцируема в точке x, а, следовательно, непрерывна в точке x, то . Тогда:

С помощью теоремы 3 можно вычислить производные функций tgx и ctgx:

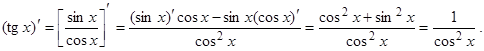Итак, получили формулу: .

Производная для ctgx находится аналогично (сделайте это):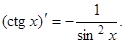

Пусть y = f(j(x)) является сложной функцией, составленной из функции
y = f (u), u = j(x), где u – промежуточный аргумент. Покажем, как найти производную сложной функции, зная производную для функции y = f (u) (ее будем обозначать через 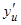) и производную 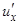для функции u = j(x).

Теорема 4. Если функция u = j(x) имеет производную 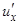в точке x, а функция
y = f (u) имеет производную 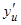в точке u (u = j(x)), то сложная функция y = f(j(x)) в точке x имеет производную , причем = .

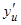
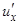Иначе, производная сложной функции равна произведению производной данной функции по промежуточному аргументу на производную промежуточного аргумента.

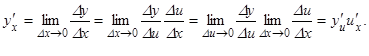Доказательство. Функция u = j(x) дифференцируема в точке x, поэтому непрерывна в этой точке, т.е. 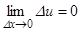(будем предполагать, что Du ¹ 0), тогда

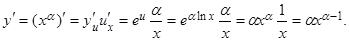С помощью теоремы 4 найдем производную степенной функции y = x^a, где
a – постоянное число. По свойствам логарифмов x^a = (e^lnx)^a = e^alnx, поэтому x^a = e^alnx является сложной функцией от x: y = e^u, u = alnx. По теореме 4:

Итак, получена формула: (x^a)' = ax^{a – 1}.

Очевидно, производные функций (найденные в разд. 2.2), могут быть вычислены по полученной формуле. В самом деле, например, для функции 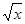имеем:

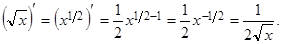
Введем правило для нахождения производной обратной функции.

Теорема 5. Пусть функция y = f(x) определена на промежутке X, непрерывна, монотонна (возрастает или убывает) и дифференцируема на X. Если ее производная в точке x не равна 0, то обратная функция x = j(y) имеет производную в точке y
(y = f(x)), причем

Доказательство. Функция y = f(x) определена, непрерывна и монотонна на промежутке X, тогда по теореме 4 (разд. 1.13) она имеет обратную функцию x = j(y), определенную, непрерывную и монотонную на промежутке Y.

Если значение аргумента y получает приращение Dy, отличное от нуля, то в силу монотонности функции x = j(y) функция x получает приращение Dx и Dx ¹ 0. В силу непрерывности функции x = j(y): .

Следовательно,

Итак, Теорема доказана.