рефераты конспекты курсовые дипломные лекции шпоры

Раздел Математика
/
Решение

Реферат Курсовая Конспект

Выберите учебное заведение

Решение

Решение - раздел Математика, ГЛАВА 2. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ 1) Dy = (X + Dx)2 – X2 = ...

1) Dy = (x + Dx)²– x²= x²+ 2xDx + (Dx)²– x²= 2xDx + (Dx)², dy = 2xDx.

2) Если x₀= 20, Dx = 0,1, то Dy = 40×0,1 + (0,1)²= 4,01; dy = 40×0,1= 4.

Запишем равенство (2.7) в виде:

Dy = dy + a×Dx. (2.9)

Приращение Dy отличается от дифференциала dy на бесконечно малую высшего порядка, по сравнению с Dx, поэтому в приближенных вычислениях пользуются приближенным равенством Dy » dy, если Dx достаточно мало.

Учитывая, что Dy = f(x₀+ Dx) – f(x₀), получаем приближенную формулу:

f(x₀+ Dx) » f(x₀) + dy. (2.10)

Пример 2. Вычислить приближенно .

Решение. Рассмотрим: f(x) = 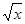; x₀= 4, Dx = 0,1; тогда = f(x₀+ Dx). Используя формулу (2.10), получим:

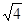= f(x₀+ Dx) » f(x₀) + dy, f(x₀) = =2, dy = f'(x₀)×Dx = ×0,1 = 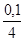= 0,025.

Значит, » 2,025.

Рассмотрим геометрический смысл дифференциала df(x₀) (рис. 2.6).

Проведем к графику функции y = f(x) касательную в точке M₀(x₀, f(x₀)), пусть j – угол между касательной KM₀ и осью Ox, тогда f'(x₀) = tgj. Из DM₀NP:
PN = tgj×Dx = f'(x₀)×Dx = df(x₀). Но PN является приращением ординаты касательной при изменении x от x₀ до x₀+ Dx.

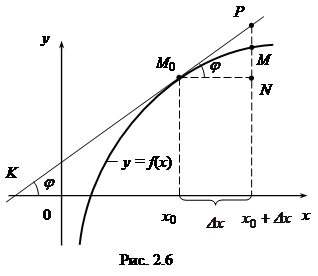Следовательно, дифференциал функции f(x) в точке x₀ равен приращению ординаты касательной.

Найдем дифференциал функции
y = x. Так как (x)' = 1, то dx = 1×Dx = Dx. Будем считать, что дифференциал независимой переменной x равен ее приращению, т.е. dx = Dx.

Если x – произвольное число, то из равенства (2.8) получаем df(x) = (x)dx, откуда (x) = или (x) = .

Таким образом, производная для функции y = f(x) равна отношению ее дифференциала к дифференциалу аргумента.

Рассмотрим свойства дифференциала функции.

Если u(x), v(x) – дифференцируемые функции, то справедливы следующие формулы:

d(u + v) = du + dv; (2.11)

d(u×v) = u×dv + v×du; (2.12)

d= 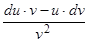, (v ¹ 0). (2.13)

Для доказательства этих формул используются формулы производных для суммы, произведения и частного функции. Докажем, например, формулу (2.12):

d(u×v) = (u×v)'Dx = (u×v' + u'×v)Dx = u×v'Dx + u'Dx×v = u×dv + v×du.

Рассмотрим дифференциал сложной функции: y = f(x), x = j(t), т.е. y = f(j(t)).

Тогда dy = 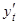dt, но 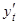= 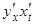, поэтому dy = 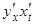dt. Учитывая,
что 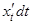= dx, получаем dy = dx = (x)dx.

Таким образом, дифференциал сложной функции y = f(x), где x = j(t), имеет вид dy = (x)dx, такой же, как в том случае, когда x является независимой переменной. Это свойство называется инвариантностью формы дифференциала.

Развернуть

Открыть в широком формате

– Конец работы –

Эта тема принадлежит разделу:

ГЛАВА 2. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ

Основные правила дифференцирования... Установим правила по которым можно находить производные суммы произведения... Теорема Если функции u x v x дифференцируемы в точке x то их сумма дифференцируема в этой точке причем...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Решение

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

Понятие производной, ее геометрический и механический смысл
Пусть функция y = f (x) определена в точке x0 и некоторой ее окрестности, x – точка из этой окрестности. Введем обозначения: разность x – x0

Решение
Если

Производные некоторых элементарных функций
Пусть функция y = f (x) определена на некотором промежутке X, x0ÎX и f(x) дифференцируема в точке x0, т.е. произв

Доказательство
Так как Du = u(x + Dx) – u(x), то u(x + Dx) = u(x) + Du.

Производные обратных тригонометрических и гиперболических функций
Используя теорему 5 (разд. 2.3) докажем следующие формулы: 1) ; 2)

Дифференцирование функций, заданных неявно. Логарифмическое дифференцирование
Пусть переменные x, y связаны между собой некоторым уравнением F(x, y) = 0, (2.1) причем y является функцией от x, тогда говорят, что функция

Функции, заданные параметрически, и их дифференцирование
Рассмотрим задание линии на плоскости, при котором переменные x, y являются функциями третьей переменной t (называемой параметром):

Дифференциал функции
Пусть функция в точке x0 имеет производную. По определению: =

Производные и дифференциалы высших порядков
Пусть функция f(x) определена и дифференцируема на некотором промежутке X, тогда ее производная (x) та

Основные теоремы о дифференцируемых функциях
Теорема Ферма. Пусть функция f(x) определена, непрерывна на интервале (a, b) и в некоторой точке x0 этого интервала принимает свое наи

Правило Лопиталя
В главе 1 мы познакомились с приемами нахождения пределов отношения двух бесконечно малых или бесконечно больших функций, т.е. раскрытия неопределенностей типа

Формула Тейлора
Формула Тейлора является одной из важнейших формул математического анализа, она имеет очень большое число теоретических и практических применений. Рассмотрим предварительно следующую задач

Возрастание и убывание функций
Теорема 1. (Достаточное условие возрастания функции) Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на интервале (

Экстремумы функции
Дадим точные определения точкам максимума и минимума функции. Пусть функция f(x) определена на промежутке X и x0 Î X. Говорят, что в точ

Выпуклость, вогнутость графика функции, точки перегиба
Пусть f(x) – функция, дифференцируемая на интервале (a, b). Рассмотрим кривую, являющуюся графиком функции y = f(x). Кривая, заданная функцией

Асимптоты
При исследовании функции часто приходится устанавливать вид ее графика (а, значит, и характер функции) при неограниченном удалении точки графика от начала координат (при стремлении переменной точки