Решение

1) Областью определения функции является вся числовая ось, за исключением точек, в которых знаменатель дроби обращается в нуль, то есть . Отсюда 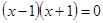, , 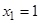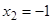. Итак, область определения .

2) Найдем :

,

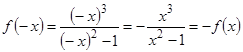так как 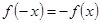, то функция 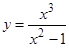является нечетной, и ее график симметричен относительно начала координат.

3) Точка пересечения с осью 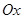определяется равенством 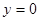, т.е.

, .

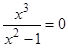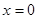Точка пересечения с осью 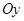определяется равенством :

,

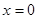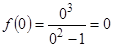т.е. 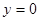. Итак, график функции имеет единственную точку пересечения с осями координат – начало координат .

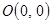4) Так как пр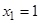и и 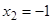не выполняется первое условие непрерывности функции в точке, то эти точки являются точками разрыва функции 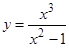. Причем эти точки являются точками разрыва второго рода, так как

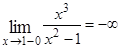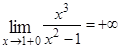, и , .

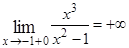5) Так как данная функция имеет точки разрыва второго рода (точки бесконечного разрыва функции), то существуют вертикальные асимптоты графика функции и их уравнения: 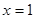и .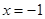

Найдем уравнения невертикальных асимптот, для этого вычислим коэффициенты в уравнении прямой :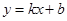

,

.

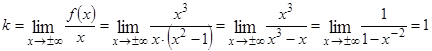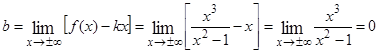Следовательно, прямая 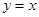является наклонной асимптотой при и .

6) Найдем производную :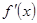

.

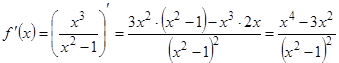Для того чтобы найти критические точки первого рода, решим уравнение: 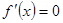и выясним, в каких точках не существует 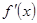. Уравнение равносильно уравнению 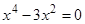или , отсюда находим стационарные точки: 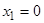, , 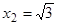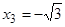. Производная не существует в том случае, когда знаменатель , т.е. при , 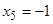. Таким образом, получили пять критических точек первого рода: , , , , .

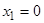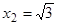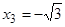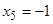7) Для нахождения экстремумов и интервалов монотонности функции на числовой прямой отметим все критические точки и определим знак производной в каждом из получившихся интервалов.

Для этого достаточно взять по одной произвольной точке из каждого интервала и вычислить значения производной (рис. 3.2).

Например: ; ;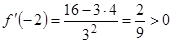

; ; ; .

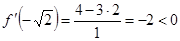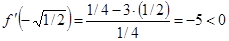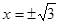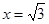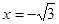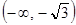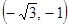Так как при переходе через критические точки производная меняет знак, то эти точки являются точками экстремума функции. В частности, при достигается минимум функции, а при – максимум. Кроме того, на интервалах и функция возрастает, а на интервалах , и
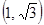– убывает.

8) Найдем :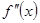

.

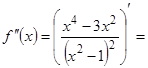
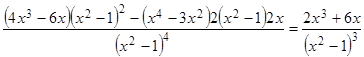Определим критические точки второго рода. Приравняем вторую производную к нулю:

,

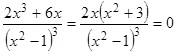это уравнение равносильно уравнению 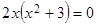, откуда .

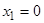Производная второго порядка не существует при . В итоге получили три критические точки второго рода: , , .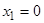

9) На числовой оси отложим все критические точки второго рода и определим знаки второй производной аналогично тому, как это сделано в пункте 7 (рис. 3.3):

, ,

, .

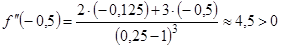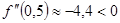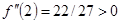При переходе через точку 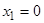вторая производная меняет знак, следовательно, – точка перегиба графика функции. На интервалах и 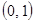график функции является выпуклым, а на интервалах 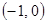и – вогнутым.

10) Вычислим значения функции в точках экстремума и перегиба:

, , .

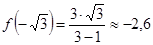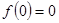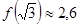Для более точного построения графика найдем значения функции в дополнительных точках: , .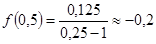

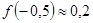11) Полученные данные занесем в таблицу:.

		(0, 1)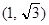
		–		–		+
		–		+	+	+

 

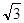
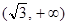
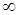
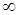
Теперь построим график функции (рис. 3.4).

Пример 2.Исследовать методами дифференциального исчисления функцию и построить ее график.