Решение
1) Областью определения функции является вся числовая ось, за исключением точек, в которых знаменатель дроби обращается в нуль, то есть  . Отсюда
. Отсюда 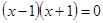 ,
, 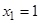 ,
, 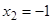 . Итак, область определения
. Итак, область определения  .
.
2) Найдем  :
:
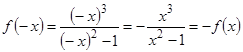 ,
,
так как 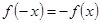 , то функция
, то функция 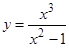 является нечетной, и ее график симметричен относительно начала координат.
является нечетной, и ее график симметричен относительно начала координат.
3) Точка пересечения с осью 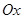 определяется равенством
определяется равенством 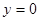 , т.е.
, т.е.
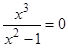 ,
, 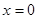 .
.
Точка пересечения с осью 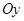 определяется равенством
определяется равенством 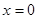 :
:
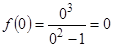 ,
,
т.е. 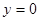 . Итак, график функции имеет единственную точку пересечения с осями координат – начало координат
. Итак, график функции имеет единственную точку пересечения с осями координат – начало координат 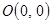 .
.
4) Так как при 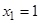 и
и 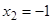 не выполняется первое условие непрерывности функции в точке, то эти точки являются точками разрыва функции
не выполняется первое условие непрерывности функции в точке, то эти точки являются точками разрыва функции 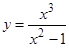 . Причем эти точки являются точками разрыва второго рода, так как
. Причем эти точки являются точками разрыва второго рода, так как
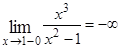 ,
, 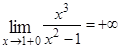 и
и  ,
, 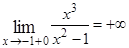 .
.
5) Так как данная функция имеет точки разрыва второго рода (точки бесконечного разрыва функции), то существуют вертикальные асимптоты графика функции и их уравнения: 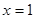 и
и 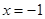 .
.
Найдем уравнения невертикальных асимптот, для этого вычислим коэффициенты в уравнении прямой 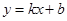 :
:
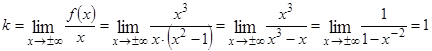 ,
,
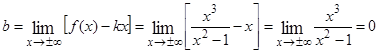 .
.
Следовательно, прямая 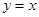 является наклонной асимптотой при
является наклонной асимптотой при  и
и  .
.
6) Найдем производную 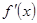 :
:
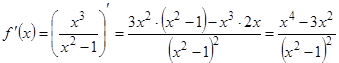 .
.
Для того чтобы найти критические точки первого рода, решим уравнение: 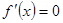 и выясним, в каких точках не существует
и выясним, в каких точках не существует 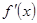 . Уравнение
. Уравнение  равносильно уравнению
равносильно уравнению 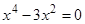 или
или  , отсюда находим стационарные точки:
, отсюда находим стационарные точки: 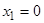 ,
, 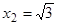 ,
, 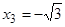 . Производная не существует в том случае, когда знаменатель
. Производная не существует в том случае, когда знаменатель  , т.е. при
, т.е. при  ,
, 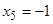 . Таким образом, получили пять критических точек первого рода:
. Таким образом, получили пять критических точек первого рода: 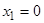 ,
, 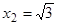 ,
, 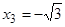 ,
,  ,
, 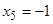 .
.

7) Для нахождения экстремумов и интервалов монотонности функции на числовой прямой отметим все критические точки и определим знак производной в каждом из получившихся интервалов.

Для этого достаточно взять по одной произвольной точке из каждого интервала и вычислить значения производной (рис. 3.2).
Например: 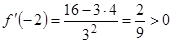 ;
; 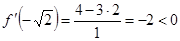 ;
;
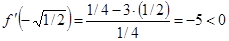 ;
;  ;
;  ;
;  .
.
Так как при переходе через критические точки 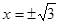 производная меняет знак, то эти точки являются точками экстремума функции. В частности, при
производная меняет знак, то эти точки являются точками экстремума функции. В частности, при 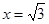 достигается минимум функции, а при
достигается минимум функции, а при 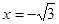 – максимум. Кроме того, на интервалах
– максимум. Кроме того, на интервалах 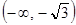 и
и  функция возрастает, а на интервалах
функция возрастает, а на интервалах 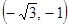 ,
,  и
и
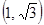 – убывает.
– убывает.
8) Найдем 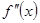 :
:
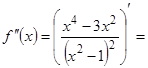
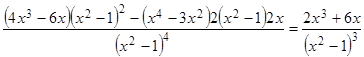 .
.
Определим критические точки второго рода. Приравняем вторую производную к нулю:
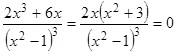 ,
,
это уравнение равносильно уравнению 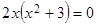 , откуда
, откуда 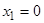 .
.
Производная второго порядка не существует при  . В итоге получили три критические точки второго рода:
. В итоге получили три критические точки второго рода: 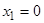 ,
,  ,
,  .
.
9) На числовой оси отложим все критические точки второго рода и определим знаки второй производной аналогично тому, как это сделано в пункте 7 (рис. 3.3):
 ,
, 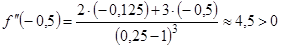 ,
,

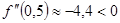 ,
, 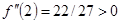 .
.

При переходе через точку 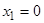 вторая производная меняет знак, следовательно,
вторая производная меняет знак, следовательно,  – точка перегиба графика функции. На интервалах
– точка перегиба графика функции. На интервалах  и
и 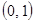 график функции является выпуклым, а на интервалах
график функции является выпуклым, а на интервалах 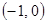 и
и  – вогнутым.
– вогнутым.
10) Вычислим значения функции в точках экстремума и перегиба:
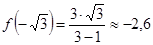 ,
, 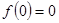 ,
, 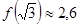 .
.
Для более точного построения графика найдем значения функции в дополнительных точках: 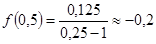 ,
, 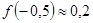 .
.
11) Полученные данные занесем в таблицу:.

| (0, 1) | 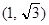
| 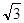
| 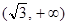
| ||

| – | 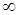
| – | + | ||

| – | 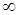
| + | + | + | |
|
Теперь построим график функции (рис. 3.4).
 |
Пример 2.Исследовать методами дифференциального исчисления функцию
 и построить ее график.
и построить ее график.