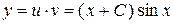Задача 5.
Найти общее решение линейного уравнения:  .
.
Уравнение вида 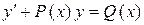 , где
, где  и
и  известные функции от
известные функции от 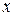 , линейное (первой степени) относительно функции
, линейное (первой степени) относительно функции  и ее производной
и ее производной 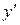 называется линейным.
называется линейным.
Посредством замены функции  произведением двух вспомогательных функций
произведением двух вспомогательных функций 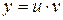 линейное уравнение сводится к двум уравнениям с разделяющимися переменными относительно каждой из вспомогательных функций.
линейное уравнение сводится к двум уравнениям с разделяющимися переменными относительно каждой из вспомогательных функций.
Уравнение Бернулли 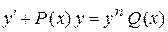 , отличающееся от линейного уравнения тем, что в правую часть входит множителем некоторая степень функции
, отличающееся от линейного уравнения тем, что в правую часть входит множителем некоторая степень функции  , решается так же, как и линейное. Посредством подстановки
, решается так же, как и линейное. Посредством подстановки 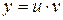 оно также сводится к двум уравнениям с разделяющимися переменными.
оно также сводится к двум уравнениям с разделяющимися переменными.
Решение. Убедившись, что данное уравнение линейное, полагаем 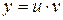 ; тогда
; тогда 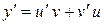 и данное уравнение преобразуется к виду
и данное уравнение преобразуется к виду
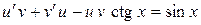
или

Так как одну из вспомогательных функций  или
или 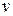 можно взять произвольно, то выберем в качестве
можно взять произвольно, то выберем в качестве 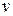 какой-либо частный интеграл уравнения
какой-либо частный интеграл уравнения 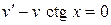 .
.
Тогда для отыскания  получим уравнение
получим уравнение 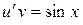 .
.
Решая первое из этих уравнений, найдем 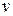 ; разделяя переменные и интегрируя, найдем его простейший, отличный от нуля частный интеграл:
; разделяя переменные и интегрируя, найдем его простейший, отличный от нуля частный интеграл:
 ;
; 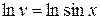 ;
; 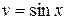 .
.
Подставляя 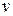 во второе уравнение и решая его, найдем
во второе уравнение и решая его, найдем  как общий интеграл этого уравнения:
как общий интеграл этого уравнения:
 ;
;  ;
; 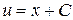 .
.
Зная  и
и 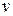 , находим искомую функцию
, находим искомую функцию  :
: