Задача 8

Найти общее решение линейного, неоднородного дифференциального уравнения с постоянными коэффициентами:

 

.

 

Линейным однородным уравнением называется уравнение

 

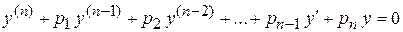, (1)

 

все члены которого первой степени относительно функции и ее производных, а коэффициенты , , … , – известные функции от аргумента 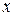или постоянные.

Общий интеграл линейного однородного уравнения 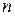-го порядка (1) имеет вид

,

где 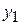, , 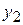… , 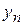– линейно независимые частные интегралы этого уравнения.

Если все коэффициенты 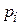линейного однородного уравнения (1) постоянны, то его общий интеграл находится с помощью характеристического уравнения

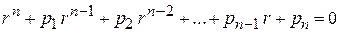, (2)

которое получается из этого уравнения, если, сохраняя в нем все коэффициенты 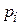, заменить функцию единицей, а все ее производные соответствующими степенями 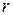. При этом:

1) если все корни , , 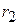… , 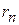характеристического уравнения (2) действительны и различны (однократны), то общий интеграл уравнения (1) выражается, формулой

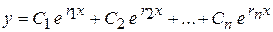; (3)

2) если характеристическое уравнение имеет пару однократных комплексных сопряженных корней 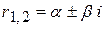, то в формуле (3) соответствующая пара членов заменяется слагаемым

;

3) если действительный корень уравнения (2) имеет кратность 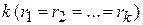, то соответствующие 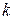членов в формуле (3) заменяются слагаемым

;

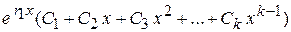4) если пара комплексных сопряженных корней 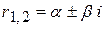уравнения (2) имеет кратность 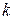, то соответствующие 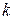пар членов в формуле (3) заменяются слагаемым

 

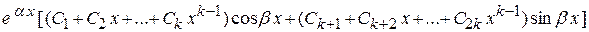
Линейным неоднородным уравнением называется уравнение первой степени относительно функции и ее производных

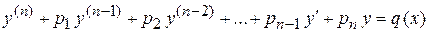, (4)

отличающееся от линейного однородного уравнения наличием в правой части некоторой известной функции 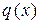от независимойпеременной .

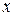Общий интеграл линейного неоднородного уравнения равен сумме какого-либо его частного интеграла 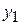и общего интеграла соответствующего однородного уравнения (получающегося из неоднородного при ).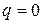

Для решения линейного неоднородного уравнения (4) с постоянными коэффициентами 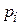вначале находится функция , затем функция 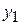. Их сумма и дает общий интеграл неоднородного уравнения: .

Для некоторых специальных видов функции 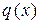частный интеграл 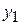можно найти методом неопределенных коэффициентов.Повиду правой части 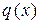можно заранее указать вид частного интеграла 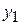, где неизвестны лишь числовые коэффициенты, и затем найти его без всяких квадратур в следующих простейших случаях:

1) , где – многочлен[1],

2) ,

3) 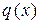есть сумма указанных функций.

В этих случаях 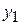есть функция, подобная 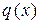, т. е. отличается от 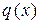только числовыми коэффициентами.

Но если число (для случая 1) или числа 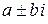(для случая 2) являются корнями характеристического уравнения кратности 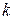, то 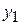отличается от 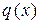множителем .

 

Решение. Вначале находим общий интеграл однородного уравнения , соответствующего данному неоднородному уравнению. Его характеристическое уравнение имеет корни 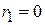, , 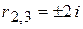поэтому общий интеграл соответствующего однородного уравнения есть

.

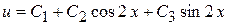Далее находим частный интеграл 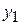данного неоднородного уравнения. Для правой части данного уравнения 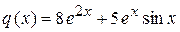, согласно указанному правилу (случаи 3, 1 и 2), 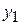есть функция, подобная 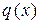, т.е.

.

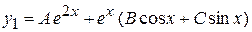Для определения коэффициентов 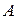, , 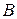находим производные

,

,

,

 

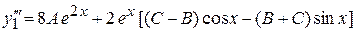подставляем и в данное уравнение:

 

 

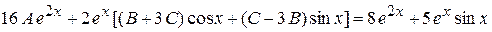
и, сравнивая коэффициенты у подобных членов, получим систему:

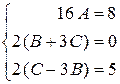из которой находим

Следовательно, ,

.